Man kann es durchaus als eine Gnade ansehen, dass es dem Menschen gegeben ist, Einblick in die Beschaffenheit der Naturgesetze zu erlangen. Dieser Einblick ist keineswegs vollständig, aber dennoch beachtlich. Albert Einstein hat es einst in seiner sprichwörtlichen Bescheidenheit so ausgedrückt: „Das Erstaunlichste ist doch, dass man überhaupt etwas verstehen kann“. Woran liegt das? Nicht wenige Naturwissenschaftler sind davon überzeugt, dass die Natur ihrem inneren Wesen nach logisch, wenn nicht sogar mathematisch angelegt ist. Und in der Tat sind fast alle bedeutenden physikalischen Naturgesetze, in der Form von mathematischen Gleichungen formuliert. Sie machen Aussagen über die Natur, die alles andere als offensichtlich sind und auch von den klügsten Köpfen nur mit Ausdauer und beharrlichem Nachdenken erschlossen werden konnten. Fünf von ihnen sollen im Folgenden näher betrachtet werden. Sie erheben den (eigentlich ungeheuren) Anspruch, an allen Orten und zu allen Zeiten gültig zu sein. Allerdings haben sie fast alle einen kleinen Schönheitsfehler: sie enthalten eine oder auch mehrere Konstanten, die nur durch Messungen festgelegt werden können. Diese sogenannten Naturkonstanten können – jedenfalls bislang nicht – durch eine Theorie erklärt werden, fallen also gewissermaßen vom Himmel. Aber, nicht jede Größe, die zeitlich konstant ist, ist eine Naturkonstante. So ist z.B. der Wert der Erdbeschleunigung (g = 9,81 m/s^2) keine Naturkonstante, weil sie keine allgemeine Aussage über die Gravitationskraft macht, sondern nur eine über die Anziehungskraft der Erde. Andererseits bezeichnet man drei in der Natur vorkommende Konstanten (c, h, G), als Fundamentalkonstanten, denn sie machen allgemeine Aussagen über Raum und Zeit und werden benötigt, um die Vielfalt der physikalischen Vorgänge im Kosmos beschreiben zu können. Insgesamt gibt es 29 Naturkonstanten *1), wovon aber im Rahmen der konventionellen Physik nur neun benötigt werden. Die übrigen 20 beziehen sich auf das Standardmodell der Elementarteilchen. 

Im Folgenden wollen wir einige Gesetze kennen lernen und die hierin auftauchenden Konstanten besprechen. Wir beginnen mit den Kraftgesetzen wie sie Isaak Newton 1686 in seiner berühmten Schrift Philosophiae Naturalis Principia Mathematica (Abb. 1) formuliert hat. Danach wenden wir uns der geistvollen Analyse des Dänen Olaf Roemer zu, der als Zeitgenosse von Newton einen ersten Beweis für die endliche Geschwindigkeit des Lichtes erbrachte. Mit der Besprechung der Gesetze der Elektrostatik und der Erörterung der Stärke der vier bekannten Kräfte soll der als Einleitung gedachte Teil abgeschlossen werden. Danach wenden wir uns dem Licht und speziell der Spektralanalyse zu, die uns die entscheidenden Informationen über die Beschaffenheit der Sterne und der Objekte am Rand des Kosmos liefert. Am Anfang dieses Abschnitts steht hier noch einmal Newton, der mit seinen genialen Leistungen auf fast allen Gebieten die gesamte moderne Naturwissenschaft geprägt hat. Den Abschluss unseres kleinen Überblicks über die Naturgesetzte bilden die vorläufig letzten Erkenntnisse zu der im Titel gestellten Frage: Sind diese Gesetze wirklich unveränderlich?

Es ist hier nicht der Ort, Newtons Gesetze in ihrer ganzen Tiefe auszubreiten. Vielmehr wollen wir uns auf seine Aussagen zur Gravitationskraft und den daraus hervorgehenden Aussagen über die Bewegung der Planeten beschränken. Johannes Kepler hatte im Jahr 1601 seine Erkenntnisse über die Bewegung der Planeten in drei Kernaussagen zusammengefasst:

• Alle Planeten umkreisen die Sonne auf elliptischen Bahnen, bei denen die Sonne in einem der beiden Brennpunkte steht.
• Die von dem Fahrstrahl Planet-Sonne überstrichene Fläche ist für gleiche Zeitintervalle gleich groß.
• Die dritten Potenzen der großen Halbachsen verhalten sich zueinander wie die Quadrate der Umlaufzeiten zweier Planeten.

Im Übrigen kann man mit diesem Gesetz alleine nicht die Bewegung der Planeten beschreiben. Man benötigt dazu noch eine zweite Kraft, die ebenfalls von Newton entdeckt wurde, und die in ihrer allgemeinen Form noch wesentlich abstrakter ausfällt. Es ist dies die Trägheitskraft mit der, der moderne Mensch vor allem als Autofahrer Bekanntschaft macht, wenn er eine Kurve durchfährt. Dann nämlich spürt er die Fliehkraft, die versucht, ihn aus der Kurve nach außen zu drängen. Diese Kraft ist für eine Kreisbahn mit dem Radius r durch die Formel Fflieh = m v^2/r gegeben. Hierin ist m die Masse des Körpers (Auto bzw. Planet) und v dessen Bahngeschwindigkeit. Die Mächtigkeit, die in diesen beiden Kraftausdrücken steckt, ersehen wir sofort, wenn wir sie gleichsetzen (Abb.  3), so dass die anziehende Gravitationskraft der Sonne auf einen Planeten gleich der abstoßenden Fliehkraft wird (Fgrav = Flieh).  Wir erhalten dann nämlich 

r v^2 = G msonne, wobei sich die Planetenmasse herausgekürzt hat. Berücksichtigen wir nun noch, dass der Planet während seiner Umlaufzeit T um die Sonne den Kreisumfang U = 2π r zurücklegt, so ist seine Geschwindigkeit v = U/T = 2π r/T und die obige Gleichung nimmt die Form r^3/T^2 = G msonne/(4π^2) = const. an, was genau die Aussage des oben angegebenen dritten Gesetzes von Kepler ist. 

Zu Newtons Zeiten war es eine wichtige Frage, ob das Licht sich mit einer endlichen Geschwindigkeit ausbreitet oder, ob es keine Zeit benötigt, um von einem Ort zu einem anderen zu gelangen, also sich mit unendlich großer Geschwindigkeit bewegt. Frühere Gelehrte, allen voran Aristoteles, aber auch Newtons Vorgänger Kepler und der große Philosoph Descartes meinten, dass das Licht unendlich schnell sei. Und in der Tat, alle Versuche, wie seinerzeit von Galilei, hatten keine messbaren Ergebnisse gezeitigt. Das änderte sich im Jahre 1676 als der Däne Olaf Roemer (1644-1710) seine sensationellen Beobachtungen veröffentlichte. 

Roemer hatte in Paris über einen längeren Zeitraum den Umlauf der von Galilei gefundenen vier Monde des Jupiters beobachtet und vermessen. Anlass war die auf Galilei zurück gehende Idee, diese Monde als himmlische Uhren zu betrachten, die insbesondere der Seefahrt hilfreiche Dienste bei der Festlegung des Längengrades auf den Weltmeeren bieten sollten. Während nämlich der Breitengrad recht gut anhand des Höhenwinkels der Sonne über dem Horizont bestimmt werden konnte, lag das Problem beim Längengrad an den Uhren. Für die Bestimmung des Längengrades musste man wissen, wie spät es zur gleichen Zeit in London, genauer in Greenwich war, wo der 0-te Längengrad durchläuft. Es gab aber praktisch keine Uhren, die auch noch nach Wochen auf See die Zeit auf die Minute genau angeben konnten *3). Bei den Jupitermonden konnte man dagegen den Transit-Zeitpunkt, d.h. wann sie aus dem Schatten des Jupiters wieder hervortraten oder in diesen eintraten, auf einige Sekunden genau messen (Abb. 4). Besonders der innerste Mond „Io“ mit einer Umlaufzeit von 42,5 Stunden schien daher als Zeitgeber geeignet. Man brauchte nur die Anzahl der Transits zu zählen, dann hatte man alle 42,5 Stunden eine genaue Zeitmarke, und für die Zeiten dazwischen reichte eine mitgeführte Uhr mit einer geringeren Ganggenauigkeit. 

Als nun aber Olaf Roemer von Paris aus sich anschickte, die Methode zu überprüfen, stellte er fest, dass es so einfach nicht war. Die Periodendauern zwischen zwei aufeinander folgenden Durchgängen waren nicht konstant. Sie nahmen zu, wenn sich die Erde von Jupiter entfernte und verkürzten sich ein halbes Jahr später bei der Wiederannäherung an ihn. Wie auf der Abb. 5 zu sehen ist, kam es nach 44 Transits zu einer Zeitdifferenz von 10 Minuten. Roemer erkannte, dass dies die Zeitdauer war, die das Licht brauchte um die Strecke zu durchlaufen, um die sich Abstand Io-Erde seit dem ersten Transit vergrößert hatte. Das war etwas weniger als der Radius der Erdbahn. Damals war allerdings dieser Radius nur in grober Näherung bekannt. Das war auch der Grund, weshalb Roemer keinen Wert für die Lichtgeschwindigkeit angab, sondern sich darauf beschränkte, die Zeit anzugeben, die das Licht benötigt, um den Erdbahndurchmesser (300 Mill. km) zu durchqueren. Dafür berechnete er aus seinen Beobachtungen 22 Minuten, was etwa um 5 Minuten zu lang ist. 

Obwohl das Phänomen der Elektrizität schon im Altertum bekannt war, begann man erst Mitte des 18. Jahrhunderts sich wissenschaftlich damit zu befassen. Durch Reiben mit Tüchern oder Fellen ließen sich Körper wie Bernstein oder Glasstäbe elektrisch aufladen, so dass sie sich gegenseitig anzogen oder auch abstießen. Charles Augustin de Coulomb war eigentlich Bauingenieur und Spezialist für militärische Festungsbauten. Im Nebenberuf beschäftigte er sich jedoch auch intensiv mit physikalischen Problemen und wurde auf Grund einer Publikation über die Theorie der Reibung 1781 in die Französische Akademie der Wissenschaften aufgenommen. In den Jahren 1785 bis 1791 verfasste er seine berühmten Abhandlungen über Elektrizität und Magnetismus. Insbesondere untersuchte er in dieser Zeit das Gesetz der elektrostatischen Kräfte mit Hilfe einer von ihm selbst gebauten Drehwaage. Das von ihm gefundene Gesetz für die Kraft mit der sich zwei punktförmige Ladungen anziehen oder abstoßen ist von ähnlichem Typ wie Newtons Gravitationsgesetz (Abb. 6). Die Kraft ist proportional zum Produkt der beiden Ladungen q1, q2 und nimmt ebenfalls mit dem Quadrat des Abstandes ab. Im Gegensatz zum Gravitationsgesetz jedoch, bei dem es nur anziehende Massen gibt, gibt es positive sowie negative Ladungen. Haben beide Ladungen das gleiche Vorzeichen, so stoßen sie sich ab, im anderen Falle, wenn sie also ungleichnamig sind, ziehen sie sich an. Die Stärke der Kraft wird durch den vorangestellten Bruch bestimmt, in dessen Nenner die Elektrische Feldkonstante εo (Zahlenwert s. Abb. 6) auftaucht. Ebenso wie die Gravitationskonstante G und die Lichtgeschwindigkeit c ist εo eine wichtige Naturkonstante. 

Abgesehen von der Möglichkeit, dass Ladungen ein negatives Vorzeichen haben können, gibt es noch einen wesentlichen Unterschied zu den Massen: Ladungen können nicht beliebig klein werden, es gibt nämlich eine Elementarladung (e), so dass jede positive Ladung ein ganzzahliges Vielfaches hiervon sein muss: q+ = n e mit n = 1, 2, 3 ... Das gleiche gilt auch für negative Ladungen q- = n (-e). Die positive Elementarladung (e) ist die Ladung des Protons, ein schweres Teilchen, das in den Atomkernen vorkommt, während die negative Elementarladung (-e), die Ladung der leichten Elektronen ist, die die Hülle der Atome bilden. Elementare Teilchen wie die Elektronen haben allesamt exakt die gleichen Eigenschaften, es sind im wahrsten Sinne des Wortes identische Teilchen, etwas, das es in der makroskopischen Natur nicht gibt. Bei den Protonen ist das schon etwas anders, denn ein Proton besteht in Wirklichkeit aus drei Quark-Teilchen, zwei up-quarks (mit jeweils der Ladung 2/3 e) und einem down-quark mit der Ladung (-e/3). Zusammen ergibt das die Ladung qp = +e, was auch so sein muss, denn sonst könnten eine gleiche Anzahl von Elektronen und Protonen keine neutralen Atome mit der Gesamtladung qa = 0 bilden. Neutronen, die mit Ausnahme des Wasserstoffatoms in allen übrigen Atomkernen auch vorkommen, setzen sich aus einem up-quark und zwei down-quarks zusammen, was insgesamt auf qn = 0 hinausläuft.

Man könnte nun auf die Idee kommen, ein Atom ist so etwas wie ein Planetensystem nur in viel kleinerem Maßstab. Was beim Planetensystem die Gravitationskraft ist, ist beim Atom die elektrische Anziehungskraft zwischen den ungleichnamigen Elektronen und Protonen. Das ist zwar nicht ganz falsch, aber beim Atom kommen noch quantenmechanischen Effekte zum Tragen, die bewirken, dass die Elektronen sich nur in ganz bestimmten Abständen zum Atomkern aufhalten können, während bei den Planeten der Abstand zum Zentralgestirn im Prinzip beliebig sein kann. 

Im Übrigen gibt es, was die Masse anbelangt, kein Pendant zur Elementarladung, also keine Elementarmasse. Abgesehen von den jeweiligen Antiteilchen haben die 17 Elementarteilchen des Standardmodells allesamt unterschiedliche Massen. Das Massenverhältnis bei den Protonen und Elektronen liegt übrigens bei mp/me = 1836,15267343. Eine Zahl, die den Physikern ebenso wie die später zu besprechende Feinstrukturkonstante ein großes Rätsel ist. 

Was nun die Stärke der elektrischen Kraft im Verhältnis zur Gravitation anbelangt, so sei auf die Abb. 7 verwiesen. Das dort erläuterte Gedankenexperiment zeigt auf, dass die elektrischen Kräfte um etwa 36 Größenordnungen überwiegen, so dass diese (mit den magnetischen zu den Elektromagnetischen Kräften zusammengefasst) – wie auf der Abb. 8 hervorgehoben – für die irdischen Verhältnisse die bedeutsamsten sind. Der vollständigkeitshalber sind dort auch die beiden übrigen Kräfte, die nur im Atomkern eine Rolle spielen, mit aufgeführt.

Über seinem Kopf schwebt der Apfel, der nach einer Legende, die der französische Philosoph Voltaire in Umlauf brachte, ihn dazu angeregt haben soll, über die Gravitationskraft nachzudenken. Newton betrachtete den Apfel, wie er vom Baum auf die Erde fiel. Äpfel fielen seit jeher von den Bäumen, das wusste ein jeder, aber warum? Dafür musste es einen Grund geben. Der Grund konnte nur eine Kraft sein, denn ohne Kraft werden die Körper nicht beschleunigt und verharren im Zustand der Ruhe, so hatte es schon Galilei erkannt. Um welche Kraft konnte es sich in diesem Fall handeln? Offensichtlich war es die gleiche Kraft, die ihn selbst auf den Boden drückte, also die Gravitationskraft. Aber sein Gesetz „actio = reactio“ (Kraft = Gegenkraft) verlangte dann, dass auch der Apfel die Erde anzog. Weil aber die Erde so ungeheuer schwer ist, merkt man es ihr nicht an, wenn sie sich ein winziges Bisschen bewegt. Vertauscht man den Apfel mit dem Mond, so müsste die Sache schon beobachtbar sein. In einem Gravitationsgesetz müssten jedenfalls die Massen beider Körper gleichberechtigt vorkommen, das heißt die Kraft muss proportional zum Produkt beider Massen sein. 

Der Mond taucht im Bild ebenfalls auf und auch das Meer, das durch ihn zu einem Berg aufgetürmt wird, so dass Ebbe und Flut entstehen. Das wussten Newtons Zeitgenossen natürlich auch. Aber warum folgten Ebbe und Flut im 6-Stunden Rhythmus aufeinander? Wenn der Mond das Meer anzog, sollte es auf der dem Mond zugewandten Seite einen Wulst bilden, der nach einer Erdumdrehung also nach 24 Stunden wiederkehrte aber nicht schon nach 12 Stunden, wie es in Wirklichkeit der Fall war. Newton löste dieses Rätsel: Wenn Erde und Mond einander umkreisen, so ist die Kraftbilanz Fgrav = Fflieh nur im gemeinsamen Schwerpunkt d.h. im Erdinnern erfüllt. Auf der Erdoberfläche treten jedoch zwei Wasserwülste in Erscheinung, einer auf der dem Mond zugewandten Seite, weil dort die Anziehungskraft des Mondes nicht völlig kompensiert ist und auf der gegenüberliegenden Seite, weil dort die Fliehkraft nicht völlig kompensiert ist. 

Links über ihm sieht man die Sonne mit ihren inneren Planeten, deren Dynamik man nun Dank seiner Bewegungsgleichungen verstehen konnte. Die dazu erforderliche Mathematik, die Infinitesimalrechnung, hatte er einige Jahre zuvor selbst entwickelt und in dem vor ihm liegenden Band der „Prinzipia Mathematica“ niedergeschrieben. Rechts vor ihm steht das von ihm gebaute erste Spiegelteleskop, das schon zu seinen Lebzeiten in ganz Europa nachgebaut wurde, weil es die hässlichen Farbverzerrungen vermied, die die bis dahin üblichen Linsenfernrohre aufwiesen. 

Was aber hält er in der Hand und wieso tritt aus diesem Glaskörper ein farbiger Strahl aus, wo doch ein weißer hineingeht? Es handelt sich dabei um ein Prisma, ein Körper aus einem durchsichtigen Material (Glas, Quarz, heute oft Kunststoff) mit einer dreieckigen Grundfläche. Newton hatte seit etwa 1700 zahlreiche optische Untersuchungen durchgeführt und gezeigt, dass das weiße Sonnenlicht mit Hilfe eines Prismas in seine Spektralfarben zerlegt werden kann, ganz so, wie das beim Regenbogen auf natürliche Weise durch Lichtbrechung an den Wassertröpfchen in der Luft geschieht. Er fand auch heraus, dass die so entstehenden Farben „rein“ sind. Lenkte er nämlich beispielsweise einen roten Strahl heraus und ließ ihn erneut durch ein zweites Prisma laufen, so blieb es bei einem roten Strahl und es erfolgte keine neuerliche Zerlegung des Lichts. 

Newton vertrat insbesondere in seinem 1704 publizierten Band „Optics“ die Auffassung, dass das Licht aus Teilchen besteht, was sofort heftig bestritten wurde. In der Tat hatte sein niederländischer Zeitgenosse Christiaan Huygens schon 1690 eine Wellentheorie des Lichtes vorgelegt, die in den folgenden zwei Jahrhunderten immer stärkere Zustimmung erfuhr. Erst im 20. Jahrhundert änderte sich die Meinung wieder, vor allem unter dem Eindruck des von Albert Einstein untersuchten Photo-Effekts (Nobelpreis 1922), der sich nur erklären ließ, wenn man Lichtteilchen (Photonen) zur Erklärung heranzog. Heute wissen wir, dass das Licht in Abhängigkeit von den experimentellen Gegebenheiten sowohl als Teilchen als auch als Welle in Erscheinung treten kann. Das gleiche gilt übrigens auch für die Elementarteilchen, nur ist bei diesen, namentlich wenn sie sehr schwer sind, diese Dualität viel schwieriger nachzuweisen.

Newton wird von seinen Zeitgenossen zwar bewundert, doch was seine charakterlichen Eigenschaften anbelangt als schwierig eingeordnet. So soll er sehr streitsüchtig und wenig kommunikativ gewesen sein. Das Letztere lässt sich erahnen, wenn man bedenkt, dass trotz der vielen Jahre, die er als Minister der Münze im Oberhaus zubrachte, nur eine einzige Wortmeldung von ihm in den Protokollen auftaucht: „Sir Newton bittet darum das obere Fenster zu schließen“. 

Übermittelt ist aber auch eine Selbsteinschätzung, die er kurz vor seinem Tode gemacht haben soll: „Ich ging am Ufer des Meeres entlang und fand einige schöne Steine.“ Wer könnte das in Zweifel ziehen?

Spektrometer und Spektralanalyse 

Die Abb. 10 verdeutlicht noch einmal, was mit dem Sonnenstrahl passiert, wenn er in das Prisma eindringt und es wieder verlässt. Ursache für die Farbzerlegung (Dispersion) ist die unterschiedliche Geschwindigkeit mit der sich die verschiedenen Farben im Kristall ausbreiten. Die zuvor angegebene Lichtgeschwindigkeit von c = 300 000 km/s bezieht sich ja auf das Vakuum in dem sich das Licht unabhängig von seiner Wellenlänge immer gleich schnell ausbreitet. In den Kristallen oder Flüssigkeiten dagegen ist sie immer deutlich kleiner als im Vakuum (z.B. im Wasser nur 0,67 c). 

Für die professionelle Spektralzerlegung benötigt man zusätzlich zum Prisma noch zwei Linsen und einen Spalt wie das in der Abb. 11 zu sehen ist. Die erste Linse verwandelt das durch den Spalt hindurchtretende divergierende Strahlenbündel in einen paralleles. Die zweite Linse dagegen macht das Umgekehrte: sie verwandelt die beiden aus dem Prisma unter leicht verschiedenen Winkeln austretenden, parallelen Bündel wieder in divergente Strahlenbüschel und fokussiert sie auf ein weißes Blatt Papier oder auch auf eine dort angebrachte Fotoplatte. Sendet die Lichtquelle nur die beiden Farben rot und blau aus, so erscheinen nun auf dem weißen Papier zwei getrennte Linien in den beiden Farben, jede in den Abmessungen des Spaltes. 

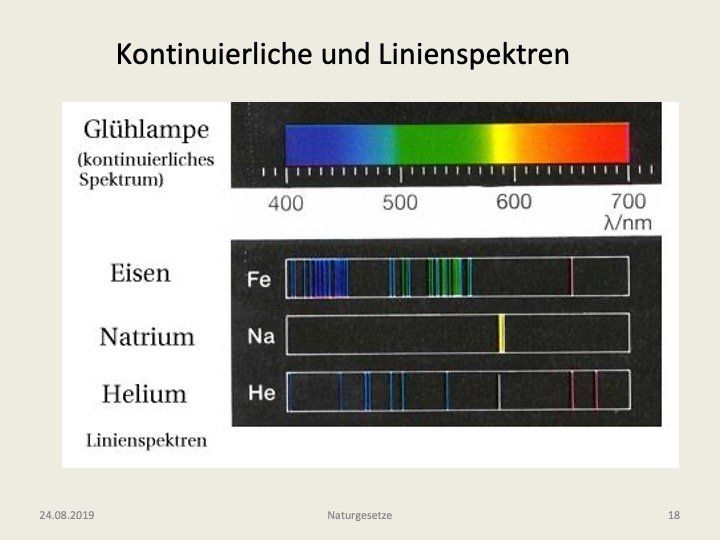
Was wir nun genau sehen, wenn die Lichtquelle eine wirklichen Kerze ist, hängt von ihrer chemischen Beschaffenheit ab. Streuen wir aber etwas Kochsalz (Na Cl) in die Flamme, so erscheint auf dem Blatt eine helle gelbe Linie, wie sie im unteren Teil der Abb. 12 abgebildet ist. Sie verrät uns, dass etwas Natrium in die Flamme gekommen ist. Vom Chlor, das ebenfalls im Kochsalz vorhanden ist, sehen wir in diesem Fall nichts, da die Kerzenflamme nicht heiß genug ist um die Chloratome zum Leuchten anzuregen. Hätten wir anstelle der Kerze aber einen Lichtbogen mit einer Eisenelektrode vor dem Spalt aufgestellt, so hätten wir das reichhaltige Linienspektrum des Eisens (Fe) gesehen. In beiden Fällen, wie auch im untersten Spektrum des Heliums, sprechen wir von einem Linienspektrum. Es besteht aus einer abzählbaren Zahl diskreter Linien, die Auskunft geben über die in der Quelle vorkommenden Atome oder auch Moleküle. 

Ein ganz anderes Spektrum erhalten wir, wenn wir anstelle der Kerze eine Glühbirne mit einer üblichen Wendel aus Wolfram oder Molybdän verwenden. Wir beobachten dann ein kontinuierliches Spektrum wie es in der Abb. 12 ganz oben gezeigt ist. Warum sehen wir in diesem Fall nicht die charakteristischen Linien der Wolfram- oder Molybdänatome? Der Grund liegt in der dichten Packung der Atome im Festkörper. Mit zunehmender Dichte der Atome kommt es nämlich zu einer Verbreiterung der Spektrallinien, so dass sie sich schließlich völlig überlappen. Das sich so ergebende Spektrum enthält keine Information mehr über die im Festkörper anwesenden Atome, wohl aber gibt es Auskunft über seine Temperatur. Derartige kontinuierliche Spektren wurden gegen Ende des 19. Jahrhunderts genauestens von Heinrich Rubens in Berlin vermessen. Als Quelle benutzte er ein hohles Metallrohr, das von außen mit einer elektrischen Wendel auf eine bestimmte Temperatur aufgeheizt wird und an einem Ende ein kleines Loch aufweist, aus dem die Strahlung austritt. Da im unbeheizten (bzw. gekühlten) Zustand das Loch am Ende völlig schwarz erscheint, nennt man die im heissen Zustand austretende Strahlung „Schwarzkörper-Strahlung“. Für das von einer solchen Quelle emittierte kontinuierliche Spektrum legte dann Max Planck im Jahre 1900 seine berühmte Gleichung vor, die die Intensitätsverteilung als Funktion der Wellenlänge (λ) und der Temperatur (T) beschreibt (s. Abb. 13). Die Verteilungen für drei verschiedene Temperaturen sind in der gleichen Abbildung wiedergegeben. Wie man sieht, liegt das Maximum für Ts = 6000 K, was näherungsweise der Oberflächentemperatur der Sonne entspricht, bei einer Wellenlänge von λ = 0,5 μm *4) und damit bei der Farbe Grün. Mit abnehmender Temperatur verschiebt sich die Lage des Maximums zu größeren Wellenlängen und liegt für die Oberflächentemperatur der Erde Te = 288 K (15°C) im unsichtbaren Infrarot-Bereich bei λ = 10 μm. Gleichzeitig schrumpft die Fläche unter der Kurve – und damit die insgesamt abgestrahlte Leistung – beträchtlich, nämlich um den Faktor (Ts/Te)^4 ≈ 2 Millionen. Derartige Informationen spielen bei der aktuellen Diskussion der Klimaproblematik eine gewichtige Rolle. Wie auch überhaupt die sich anschließende Erörterung der Strahlungs-Emission- und Absorption für das Verständnis der Vorgänge in der Atmosphäre von hoher Relevanz ist. Zunächst wollen wir aber uns noch etwas näher mit der Planckschen Formel befassen. Planck hatte sie zunächst empirisch entwickelt und festgestellt, dass sie die Messungen von Rubens sehr gut beschrieb, aber was war die Physik dahinter? Diese Frage beschäftigte ihn viele Monate. Schließlich kam er zu dem Schluss, dass er sie nur erklären konnte, wenn er annahm, dass Energie nicht in beliebig kleinen Portionen übertragen werden kann. Licht der Wellenlänge λ bzw. der Frequenz ν=c/λ besteht aus Photonen (Lichtteilchen), wobei jedes Photon die Energie h ν besitzt. Die Größe h, das sogenannte Plancksche Wirkungsquantum, hat den Wert 6,6260⋅10^(−36) Js . Wie bereits eingangs erwähnt, ist die Größe h zusammen mit c und G eine der drei Fundamentalkonstanten der Natur. 

Niels Bohr, der große Atomphysiker, kommentierte diese revolutionäre Entdeckung einige Jahrzehnte später mit der Bemerkung: „Es gibt wohl wenige Ereignisse, die so außerordentliche Erfolge gehabt haben wie Plancks Entdeckung“. Jedenfalls war mit der Publikation dieser Formel der Auftakt zur Entwicklung der Quantentheorie gemacht, der sich bis etwa 1935 hinziehen sollte. 

86 Jahre zuvor hatte Joseph Fraunhofer in München eine merkwürdige Entdeckung gemacht. Er war zunächst als Linsenschleifer ausgebildet worden, hatte sich aber dann im Selbststudium fortgebildet und leitete bereits um 1810 im Alter von 23 Jahren ein optisches Labor mit 50 Angestellten. 1814 hatte er ein neuartiges Spektrometer fertiggestellt, das anstelle des Prismas ein sogenanntes Gitter aufwies, eine Glasplatte in die er mit einer Ritzmaschine 20 000 feine Furchen geritzt hatte. Dieses Gitter zerlegte ebenso wie ein Prisma weißes Licht in seine Farbanteile, nur mit deutlich höherer Auflösung. Als er mit diesem Apparat zum ersten Mal das Licht der Sonne analysierte, entdeckte er etwas Merkwürdiges: Im farbigen Spektrum tauchten feine schwarze Linien auf. Er erkannte sofort, dass diese dunklen Linien wichtige Informationen über die Sonne enthalten mussten. Sein Ausspruch: „Diese schwarzen Linien sind die Hieroglyphen, in denen der Sonnengott seine eigene Geschichte geschrieben hat“, bringt dies klar zum Ausdruck. Da es zur damaligen Zeit noch keine Farbphotographie gab, machte er sich persönlich an die Arbeit und übertrug mit großer Sorgfalt per Hand 500 schwarze Linien von dem vor ihm liegenden Bild der Projektion in eine Kopie, in der er zuvor den farbigen Hintergrund angelegt hatte (s. Abb. 14). Darüber zeichnete er auch eine Kurve, die nach seinem Helligkeitsempfinden die Intensitätsverteilung wiedergab. Er hatte damit die Planckfunktion 86 Jahre vor ihrer mathematischen Formulierung intuitiv erfasst. Nicht zu Unrecht kann man daher das Jahr 1814 als das Geburtsjahr der Astrophysik ansehen. 

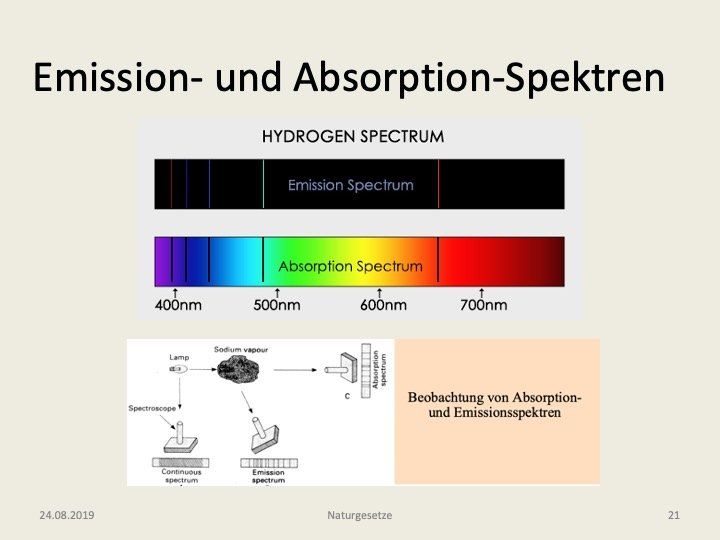
Das Verständnis, wie es zur Entstehung der schwarzen Fraunhofer-Linien kommen kann, ist für das Weitere von großer Bedeutung. Grundsätzlich ist es so, dass die Spektren der Fixsterne sowohl helle Linien (man nennt sie Emissionslinien) als auch dunkle Linien (Fraunhofer- oder Absorptionslinien) aufweisen können. Ein Beispiel dafür zeigt die Abb. 15, die im oberen Teil das Emissionsspektrum von Wasserstoff und darunter das entsprechende Absorptionsspektrum wiedergibt. Im unteren Teil der Folie ist nun die Erklärung für diese Dualität gegeben. Anstelle von Wasserstoff hier jedoch für Natrium. In der Realität kann man sich die dort skizzierte Na-Wolke so vorstellen, dass etwas Natrium in eine Glasröhre gefüllt wird und diese dann erhitzt wird. Links hat man eine gewöhnliche Glühwendellampe, die, wie wir schon früher festgestellt haben, ein kontinuierliches Spektrum ausstrahlt. Dringt dieses Licht nun in die Natriumwolke ein, so kann es die Natriumatome anregen, wobei ein Elektron durch Absorption eines Photons in einen höheren Energiezustand befördert wird; es springt dabei, anschaulich gesprochen, auf eine weiter außen liegende Bahn. Nach einer sehr kurzen Zeit (etwa 10^-8 s) fällt es jedoch wieder von alleine in den vorherigen Grundzustand zurück, und sendet dabei ein Photon der gleichen Wellenlänge wieder aus, diesmal jedoch ist die Richtung beliebig, so dass man auch unter 90° zur ursprünglichen Richtung jetzt das gelbe Licht des Natriums beobachten kann. Dieses Streulicht (Fluoreszenzlicht genannt) erzeugt also ein Emissionsspektrum, wenn wir die Natriumwolke von der Seite her betrachten. In Durchgangsrichtungsrichtung dagegen fehlen nun die seitlich abgestrahlten Photonen und man beobachtet eine schwächere Intensität bei der gleichen Wellenlänge – es entsteht eine Absorptionslinie.

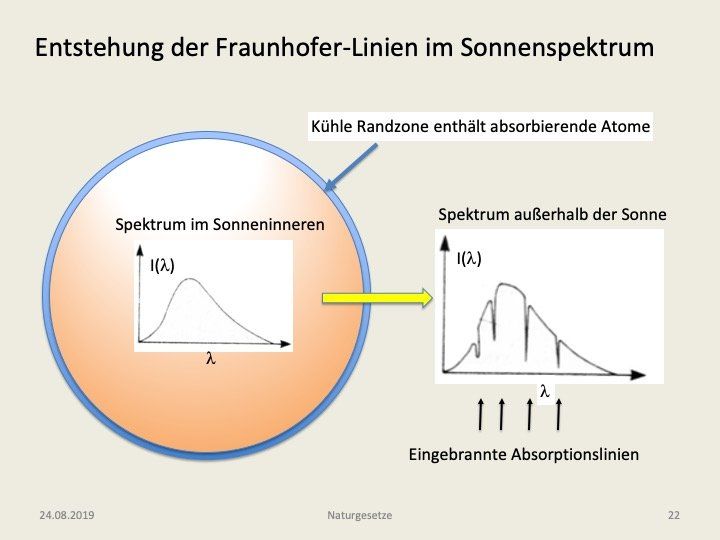
Wir sollten nunmehr auch in der Lage sein, die Entstehung der Fraunhofer-Linien im Sonnenspektrum zu begreifen. Im Inneren der Sonne und auch noch in den heißen Randzonen haben wir eine sehr hohe Temperatur und eine sehr hohe Teilchendichte, es bildet sich dort also ein Strahlungskontinuum aus, wie es in der Abb. 16 skizziert ist. Dringt diese Strahlung aber in die sogenannte Chromosphäre ein, eine äußere kalte Zone mit einer Temperatur von nur etwa 4000 K, so werden die dort vorhandenen Atome von der Kontinuums-Strahlung zum Leuchten angeregt und es passiert genau das, was wir soeben bei der Natriumwolke diskutiert haben: im Durchgangslicht treten Absorptionslinien auf. Bei einer totalen Sonnenfinsternis kann man übrigens auch die Sonnenchromosphäre in Emission beobachten. In diesem Fall wird ja die innere Zone der Sonne vom Mond ausgeblendet und man schaut tangential auf diese dünne Schicht, die man schon mit bloßem Auge im grünlichen Licht leuchten sieht.

Mit der fortschreitenden Verbesserung des Auflösungsvermögens der Spektrometer stellte sich heraus, dass eine Reihe von Spektrallinien, in Wirklichkeit Zwillinge oder Drillinge, wenn nicht gar Vierlinge sind. Das in der Abb. 17 gezeigte Sonnenspektrum offenbart uns beispielsweise, dass die von Fraunhofer als D klassifizierte Linie des Natriums in Wahrheit ein Dublett ist. 

Die Ursache für diese Feinstruktur liegt in einer quantenmechanischen Eigenschaft der Elektronen begründet. Elektronen besitzen nämlich nicht nur eine elektrische Ladung, sondern darüber hinaus auch einen Eigendrehimpuls. Ähnlich wie die Erde neben einem Bahndrehimpuls, der durch den Umlauf um die Sonne zustande kommt, noch einen Eigendrehimpuls infolge der Erddrehung um ihre Nord-Süd-Achse aufweist, gibt es bei den Elektronen ebenfalls diese zwei Drehimpulsarten. Während man sich allerdings die Erde auch nicht-rotierend vorstellen kann, ist der Bahndrehimpuls der Elektronen, hier Spin genannt, eine ihnen von der Natur zugewiesene Eigenschaft, die ihnen immerzu immanent ist: der Spin ist immer da und hat für alle Elektronen den gleichen Wert (0,5 h/2π ). Mit ihm verbunden ist ein kleiner magnetischer Dipol, der sich in einem äußeren Magnetfeld ausrichten kann. Dabei gibt es nur die zwei Möglichkeiten: parallel oder antiparallel zur Feldrichtung. Im Atom gibt es aber immer schon ein magnetisches Feld, welches durch den Bahndrehimpuls zustande kommt. Eine umlaufende elektrische Ladung ist nämlich äquivalent zu einem elektrischen Kreisstrom und ein solcher erzeugt ein Magnetfeld, das senkrecht zur Kreisebene gerichtet ist. Zugegeben, dies ist nicht einfach zu verstehen, kann aber genauestens berechnet werden. Die Konsequenz ist jedenfalls eine sogenannte Spin-Bahn-Kopplung der Elektronen, die zu einer kleinen Energiedifferenz führt, je nachdem in welcher der beiden möglichen Richtung der Spin sich ausrichtet. Für das Wasserstoffatom wurde diese Berechnung erstmalig von Arnold Sommerfeld im Jahre 1916 durchgeführt. Er fand heraus, dass die Aufspaltung durch eine dimensionslose Zahl charakterisiert ist, die eine Kombination von vier anderen Naturkonstanten darstellt α = e^2 /(2 εo h c), und näherungsweise den Wert α ≈ 0,0729 = 1 /137 aufweist (Abb. 18). Diese Sommerfeldsche Feinstrukturkonstante  ist gleichzeitig eine Maßzahl für die Stärke der Elektromagnetischen Wechselwirkung. Zum Glück ist ihr Wert erheblich kleiner als 1, da sonst viele Zusammenhänge noch wesentlich schwieriger zu verstehen wären. Ja, schlimmer noch, wir würden wahrscheinlich erst gar nicht über sie nachdenken können, denn wenn der Wert um etwa 5% von dem obigen abweichen würde, würde es die Welt, wie sie ist, gar nicht geben.   

Natürlich setzt das zunächst eine genaue Kenntnis des aktuellen Wertes von auf der Erde (αo) voraus. Diese Kenntnis ist gegeben, man kennt αo mit einer Genauigkeit von 10 Dezimalstellen (R. Parker 2018). Sodann kann man die Linienaufspaltung der interessierenden Atome ebenfalls sehr genau im Labor vermessen. Weiterhin braucht man die mathematischen Gleichungen wie sich diese Aufspaltungen verändern, falls α ≠ αo. Diese Berechnungen sind durchgeführt worden und liegen in der Form tabulierter Funktionen für die relevanten Atome und Ionen vor (s. Uzan 2003, S. 14). Schließlich benötigt man noch die geeigneten Objekte. Das sollten möglichst solche sein, die sauber getrennte Absorptionslinien aufweisen. Absorptions-Spektren sind den Emissionsspektren insofern überlegen, als hier die Linienzahl geringer ausfällt und die Linien selbst weniger stark verbreitert sind. Schließlich braucht man dann auch noch das hochauflösende Equipment: ein lichtstarkes Teleskop und ein hochauflösendes Spektrometer.

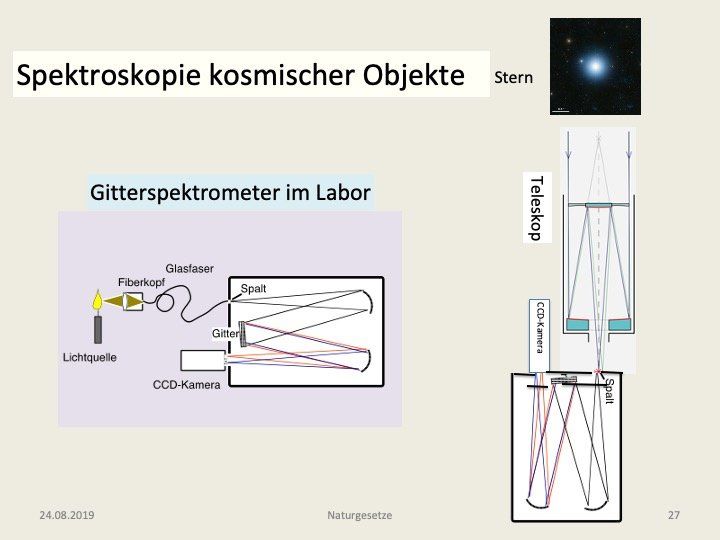
Wie man deratige Messungen zumindest im Prinzip an Sternen, Galaxien und Quasaren durchführt ist in der Abb. 19 erläutert. Hier ist zunächst der Aufbau eines modernen Gitterspektrometers für den Einsatz im Labor illustriert. Dabei wird das zu analysierende Licht im Fiberkopf mit einer Linse auf einen flexiblen Lichtleiter fokussiert, der das Licht zum Eingangsspalt des Spektrometers (hier vom Typ: Cerny-Turner) transportiert. In etwa 1 bis 3 m Entfernung befindet sich ein Parabolspiegel, der das divergente Strahlenbündel in ein paralleles verwandelt. Das parallele Licht fällt dann auf das Gitter das typischerweise 1000 Ritze pro mm und insgesamt etwa 100 000 Ritze aufweist. Das dort dispergierte Licht wird auf den zweiten Parabolspiegel reflektiert, der es auf die Ebene des Austrittspaltes fokussiert. An Stelle eines Spaltes ist dort nun eine CCD-Kamera (CCD: Charged-Coupled-Divice) angebracht, die, ähnlich wie eine moderne Digitalkamera ein zweidimensonales Bild der Spektren erstellt und die Daten im vorgegebenen Zeittakt an einen Computer oder ein Speichermedium weiterleitet. 

Dieses Spektrometer kann man nun mit einem Teleskop zusammenkoppeln, wie es auf der rechten Seite der Abb. 19 gezeigt ist. Hier handelt es sich um ein Cassegrain-Teleskop, das sich durch eine hohe Lichtstärke auszeichnet. Das vom Stern ausgesandte Licht fällt dabei zunächst auf einen durchbohrten Hohlspiegel an der Rückwand des Teleskops. Nach einer weiteren Reflexion an dem convexen Spiegel auf der Teleskopachse trifft es dann als fokussiertes Strahlenbündel auf den Eintrittsspalt des Spekrometers.

Relevante spektroskopische Untersuchungen wurden in erster Linie von einer australischen Forschergruppe an den beiden Keck-Teleskopen auf Hawaii durchgeführt (J.K. Webb, 2011). Ergänzende Messungen kamen vom Very Large Teleskop (VLT) in Chile. Es wurden sowohl die Spektren von zahlreichen Galaxien als auch von 150 Quasaren aufgenommen (s. Abb. 21). Quasare (QSO = Quasi Stellar Object) sind Galaxien, die im sichtbaren Licht wie ein punktförmiger Stern erscheinen. In der Mitte eines Quasars befindet sich in der Regel ein sehr großes Schwarzes Loch, das von einer Scheibe hell leuchtender Materie umgeben ist. Sie zählen daher zu den leuchtkräftigsten Objekten im gesamten Universum. Ihr Licht kann auch noch bei extremer Entfernung spektroskopisch analysiert werden. Einige von ihnen sind von einer relativ kühlen Gaswolke umgeben und zeigen daher die zuvor besprochenen Absorptionslinien auf hellem Hintergrund. Allerdings sind die Spektren wegen der großen Fluchtgeschwindigkeit, die, wie Hubble schon vor über 90 Jahren feststellte, proportional zur Entfernung zunimmt (v = H r), sehr stark ins Rote verschoben. Diese, durch den Doppler-Effekt hervorgerufene Rotverschiebung, bereitet jedoch keine grundsätzlichen Probleme, da man sie leicht durch eine mathematische Transformation berücksichtigen kann.

In der angeführten Analyse hatten einige Objekte eine Entfernung von 11 Milliarden Lichtjahren. Das heißt, wir sehen sie jetzt im Zustand etwa 2,7 Milliarden Jahre nach dem Urknall, der vor etwa 13,7 Milliarden Jahren stattfand. Es sind Objekte am Rande des uns zugänglichen Universums. Das von diesen Quasaren ausgestrahlte Licht war 11 Milliarden Jahre unterwegs bevor es auf der Erde eintraf und gibt uns nun Auskunft darüber gibt, wie die Welt damals beschaffen war. Zunächst ist es interessant festzustellen, dass es damals schon die gleichen Atome gab, wie wir sie auch heute auf der Erde und im gesamten Sonnensystem finden. Die Feinstrukturaufspaltung und damit die Feinstrukturkonstante wurde anhand von Alkali-Atomen (Li, Na, K) als auch an den Atomen von Eisen, Nickel, Magnesium, Silber und Zinn bestimmt. In einer ersten Zusammenfassung kann man sagen, dass die Abweichungen zum heutigen Wert kleiner als 0,001% sind. Mathematisch präzise ausgedrückt heißt das (α - αo)/αo ≤  1 ⋅10^-5, was zunächst eine sehr solide Aussage über die Konstanz des Wertes ist. Auf das Jahr bezogen heißt es, dass innerhalb eines Jahres der Zahlenwert der Größe α um weniger als 

Es soll jedoch nicht verschwiegen werden, dass die Autoren (J.K. Webb, 2011) dennoch glauben, in ihren Daten einen kleinen, aber signifikanten Unterschied zwischen der südlichen und der nördlichen Himmelssphäre ausmachen zu können. Die wissenschaftliche Fachwelt ist zurzeit noch sehr unentschieden, ob sie diesen Unterschied, der unterhalb des oben angegebenen Grenzwerts liegt, anerkennen soll. Man wartet daher auf weitere neuere Untersuchungen, die hoffentlich mehr Sicherheit bringen.

Schon seit langem fragt sich die physikalische Gemeinschaft, ob uns der Zahlenwert der Feinstrukturkonstanten, den wir ja sehr genau kennen, einen Hinweis gibt, was im Urknall geschehen ist. Handelt es sich um eine reine Zufallszahl oder musste sie zwangsläufig den Wert annehmen, den wir nun über Milliarden von Jahren hinweg konstatieren. Diese Frage drängt sich umso mehr auf, als wir ja wissen, dass der Wert nicht viel anders hätte ausfallen dürfen, damit wir uns noch heute den Kopf über ihn zerbrechen können. 

Aber andres gefragt, wann würde uns die Zahl einen Hinweis darauf geben, dass sie keine Zufallszahl ist. Nun, wenn etwa 1/α den Wert 100 hätte, wäre das gewiss äußerst erstaunlich, denn die Zahl 100 bezieht ihre Bedeutung allein aus dem Umstand, dass der Mensch 10 Finger hat, und da es den Menschen im Augenblick des Urknalls noch nicht gab, wäre es völlig hoffnungslos, mit diesem Wert eine sinnvolle Korrelation herzustellen zu wollen. Anders sähe es jedoch aus, wenn 1/α den Wert 43 π = 135,088… hätte, denn 43 ist eine Primzahl und die Kreiskonstante π ist das Verhältnis von Kreisumfang zu Durchmesser. Damit wäre die Geometrie schon im Urknall dabei gewesen, was ein deutlicher Hinweis wäre, dass schon ganz zu Anfang die Mathematik oder allgemeiner die Logik eine Rolle gespielt hätte. 

Werner Heisenberg, der bedeutende Quantentheoretiker, hat kurz nachdem Sommerfelds Konstante bekannt wurde, einen ähnlichen Versuch mit der Zahl π unternommen. Sein Ergebnis ist in der Abb. 21 angegeben (s. H. Fritsch, S. 35). Es liefert zwar die ersten drei Ziffern korrekt, aber schon die erste Nachkommastelle ist falsch. Deutlich besser ist der auf den Mathematiker Wyler zurückgehende Ansatz, der auch die ersten drei Nachkommastellen richtig angibt. Allerdings wirkt hier der zugrunde gelegte Ansatz mit zwei komplizierten Faktoren sehr gekünstelt. 

Schließlich hat auch der Autor dieser Zeilen sein Glück versucht. Dabei hat er sich davon leiten lassen, dass neben der Zahl π der Eulerschen Zahl e = 2,718…, eine ähnliche Bedeutung zukommt, da sie bei allen Wachstums- und Zerfallsprozessen eine Rolle spielt. Mit dem Produktansatz 

   w ={r^n1 π^n2 e^n3} mit ni ={−3,− 5/ 2 ,−2,− 3 /2 ,−1,− 1 /2 ,0,+ 1 /2 ,+1,+ 3/ 2 ,+2,+ 5/ 2 ,+3} und i = 1,2,3

worin r die Menge aller Brüche (rationale Zahlen) im Bereich 1/17 < r < 18 und mit der Einschränkung, dass alle Nenner kleiner als 17 sind, werden dann alle 1 737 658 Elemente der Menge w mit dem Computer berechnet. Hiervon erfüllen genau 20 die Bedingung, die Zahl 1/α mit einer relativen Genauigkeit besser als 0,5 ⋅10^-4  zu reproduzieren. Nur zwei davon 

                                                   9604π /81e = 137,032    und    (47 /6)  π^( 5/2) = 137,032

erreichen eine Annäherung an den korrekten Wert 137,035999046, wo die zweite Stelle nach dem Komma noch richtig ist. Das ist insgesamt ein entmutigendes Ergebnis. Andere mögen jedoch mit neuen Ideen erfolgreicher sein.

 

*3) Temperaturen werden in der Physik grundsätzlich in der Einheit Kelvin (K) angegeben. Der absolute Nullpunkt liegt dann bei T = 0 K = - 273°C. Dem Celsiuswert 0°C entsprechen demnach T= 273 K. Temperaturdifferenzen haben im Kelvin- und Celsius-Maß den gleichen Zahlenwert. In der Planckformel kommt T als Produkt mit der Boltzmann-Konstanten kB vor. Letztere ist ebenfalls eine Naturkonstante, der aber im Folgenden keine Bedeutung zukommt.

Harald Fritsch, Das absolut Unveränderliche, Piper Verlag

J. K. Webb, J. A. King, M. T. Murphy et al., Indications of a spatial variation of the fine structure constant. arXiv:1008.3907v2 [astro-ph.CO] 1 Nov 2011

VLT

Jean-Philippe Uzan, 2003, The fundamental constants and their variation: observational status and theoretical motivations, 

arXiv:hep-ph/0205340 

Richard H. Parker, Chenhui Yu, et al., Measurement of the fine structure constant as a test of the Standard Model, Vol. 360, Issue 6385, pp. 191-195, DOI: 10.1126/science.aap 7706

E. Peik, B. Lipphardt, H. Schnatz, New limit on the present temporal variation of the fine structure constant. 

arXiv:physics/0402132 [physics.atom-ph]