Gerd Fussmann Physik und Vorträge

Macht und Zauber der Symmetrie in Wissenschaft und Kunst

1. Einführung

Eigentlich weiß ja ein jeder, was mit Symmetrie gemeint ist. Doch fragt man nach, so erhält man die unterschiedlichsten Antworten. Der klassisch Gebildete etwa sagt: „Der Begriff Symmetrie kommt aus dem Griechischen und kann mit Ebenmaß übersetzt werden“. Aber was ist Ebenmaß? Diejenigen, die eine mathematisch naturwissenschaftliche Ausbildung durchlaufen haben, mögen dagegen antworten: „Symmetrie ist die Eigenschaft eines Körpers auf sich selbst abgebildet werden zu können.“ Alles klar?

Ich möchte mich aber jetzt nicht gleich zu Anfang am Begrifflichen festbeißen, sondern zunächst einfach einen Blick auf den Hintergrund der ersten Folie werfen ( Abb. 1 ). Er stammt von Hans Peter Reuter. Er hat das Bild 1979 geschaffen und ihm den Titel Lichthof gegeben. Die linke Hälfte ist deckungsgleich mit der rechten, es handelt sich um eine Spiegelung an der Mittelsenkrechten. Wir sprechen deshalb von einer bilateralen Symmetrie. Der Symmetrie-Eindruck wird in diesem Fall durch die Rasterung verstärkt. Der Künstler sagt dazu: „Das Raster hilft mir, die Welt zu strukturieren. So wird sie übersichtlicher und schöner.“ Damit hat er gleich zwei wichtige Eigenschaften genannt, die mit der Symmetrie verbunden sind: Sie ordnet und verschönt unsere Welt.

2. Zauber der Symmetrie

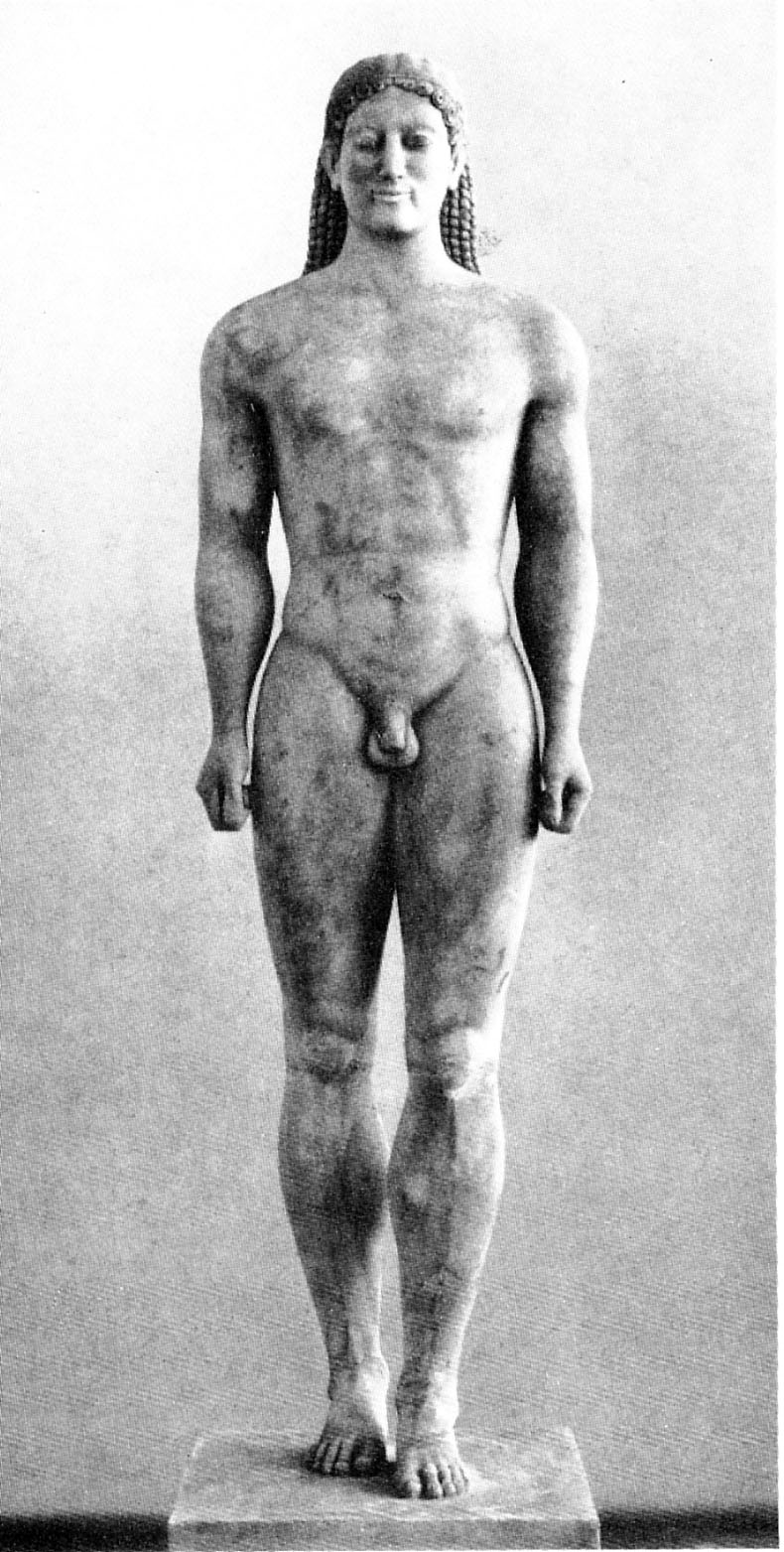
Ich möchte mich nun zunächst mit dem Schönheitsaspekt befassen, der mir persönlich als ein echtes Zaubermittel erscheint. Es ist ein Zauber, den nicht nur der darstellende Künstler verwendet, auch der Musiker, der Dichter, der Architekt, ja sogar die Natur selbst, ob nun in ihrer belebten oder unbelebten Form, bedient sich seiner allenthalben. Schauen wir uns nun einige Beispiele an. Im zweiten Bild

(Abb. 2 ) sehen wir die Statue eines jungen Mannes, wie sie in der Zeit 600 bis 400 v. Chr. vor allem als Grabstatue im klassischen Griechenland zahlreich Verwendung fand. Man bezeichnete derartige Statuen als Kouros; das weibliche Pendant, die Kore, war ebenfalls sehr beliebt. Allen war eine strenge, bilaterale Symmetrie vorgegeben. Diese wurde als Ausdruck der Stärke und Leistungsfähigkeit angesehen. Asymmetrien dagegen, etwa im Gesichtsbild oder in der Körperhaltung, wurden als Zeichen des Alters gedeutet. Charakteristisch für eine Kouros-Statue ist ferner eine ausgeprägte, wenngleich nicht übermäßig betonte Muskulatur als auch eine jugendliche Frische, die durch ein angedeutetes Lächeln überzeugt. Die zu Fäusten geballten Hände drücken Entschlossenheit und Mut aus. Alle Gliedmaßen sind wohl proportioniert: Keine Frage, es ist ein Idealbild eines schönen Menschen.

Die Abb. 3 zeigt uns eine persische Glasurfliese aus dem 19. Jh.: König Khosrow und seine Geliebte Shirin zu Pferde bei der Falkenjagd. Wiederum gewinnt die Darstellung durch die symmetrische Anordnung, wenngleich diesmal die bilaterale Symmetrie nicht in aller Strenge eingehalten wird. Eine Besonderheit liegt in der Vertauschungs-Symmetrie, die im oberen Teil des Bildes zu besichtigen ist. Um diese zu verstehen, muss man wissen, dass der König ein Anhänger des alt-iranischen Propheten Zarathustra, seine Geliebte hingegen Christin war. Im oberen Bildteil ist jedoch die Zuordnung der Gotteshäuser vertauscht: Bei der Christin sieht man eine Moschee, beim König dagegen eine Kirche. Ähnliche Vertauschungs-Symmetrien waren auch in der Dichtkunst sehr beliebt. Hier sei nur kurz angemerkt, dass Vertauschungsrelationen auch in der Quantenmechanik im Zusammenhang mit der Heisenbergschen Unschärferelation eine bedeutende Rolle spielen.

Die folgenden zwei Bilder zeigen Beispiele für eine radiäre Symmetrie. Abb. 4a eine sogenannte Fensterrose aus dem 12. Jh. an der Kirche St. Etienne in Beauvais im Norden Frankreichs. Kirchenfenster dieser Art waren im Mittelalter weit verbreitet. Nach der damals vorherrschenden scholastischen Philosophie steht das Symbol des Rades symbolisch für die Welt und die Gesetzmäßigkeit im Kosmos. Abb. 4b eine moderne Fensterrose in der Kathedrale von Palma de Mallorca, geschaffen von Antonio Gaudi Anfang des 20. Jh. Der Blick auf das kreissymmetrische Fenster soll die Andacht beim Gebet unterstützen.

Die folgenden Bilder, Abb. 5 und Abb. 6 , zeigen Beispiele für radiäre Symmetrie in der Pflanzen- und Tierwelt. Links ein Foto eines Seeigels mit Rosettenstruktur. Rechts ein Beispiel aus der 500 Arten umfassenden Gruppe der wunderschönen Passionsblumen: die 10-zählige Rosette der „Passiflora ambigua“ mit fünf Staubgefäßen und drei Narben in der Mitte. Mit der Abb. 7 folgt noch eine fein ausgeklügelte Graphik mit 4-zähliger Symmetrie von Viktor Vasarely aus dem Jahre 1971. Hier sind sowohl Mittelsenkrechte als auch die Mittelwaagerechte Symmetrie-Spiegellinien. Schließlich sehen wir in der Abb. 8 einen Schneekristall mit 6-zähliger Symmetrie. Es ist ein Beispiel für eine diskontinuierliche Symmetrie. Dreht man das Bild um 360°/6=60° oder ein ganzzahliges Vielfaches davon, so ist es wieder mit dem ursprünglichen identisch. Man kann es also durch eine Symmetrieoperation (hier Drehung) auf sich selbst abbilden. Allgemein beträgt der Drehwinkel bei einer n-zähligen Symmetrie α =360°/n. Für n→∞ wird dann α = 0; man nennt diesen sehr wichtigen Fall, wo keine Winkelabhängigkeit mehr vorliegt, isotrop und spricht von kontinuierlicher Symmetrie. Schon Johannes Kepler, der berühmte Astronom, von dem noch im Folgenden die Rede sein wird, hat sich die Frage gestellt, warum die Schneeflocke ausgerechnet eine 6-zählige Symmetrie annimmt. Er vermutete einen Zusammenhang mit den Honigwaben, die ja ebenfalls eine sechseckige Struktur aufweisen, konnte aber letztlich das Rätsel nicht lösen. Heute wissen wir, dass bei der Schneeflocke die Symmetrie durch die Struktur des Wassermoleküls H2O vorgeben wird. Allerdings kann eine Schneeflocke im Detail sehr verschieden aussehen. Mindestens 5000 verschiedene Formen sind bislang dokumentiert. Es hängt nämlich sehr davon ab, welches Milieu (Temperatur, Feuchtigkeit, Strömung etc.) sie beim Fall aus den Wolken vorfindet. Was nun die Honigwaben angeht, so ist auch dort die Symmetriefrage nicht so einfach zu beantworten, denn keineswegs sind die Bienen selbst in der Lage, Waben mit dem in Abb. 9a gezeigten sechseckigem Querschnitt herzustellen. Sie bauen vielmehr zunächst Waben mit kreisförmigem Querschnitt wie in Abb. 9b gezeigt. Im Laufe der Zeit aber, nehmen diese die hexagonale Gestalt an, die insofern eine Verbesserung darstellt, als nun der verfügbare Raum viel besser ausgenutzt wird. Ob die Bienen selbst aktiv an dieser Verbesserung beteiligt sind, indem sie etwa in großer Zahl in ihrem Stock herumfliegen und dadurch das Wachs erwärmen und somit erweichen, ist nach Wissen des Autors noch nicht bewiesen.

Zum Abschluss dieser Einführung seien noch zwei Beispiele aus der Welt der Moleküle erwähnt. Bekannt geworden durch einen Traum ist das in Abb. 10 illustrierte Benzolmolekül. Es gehört zur Gruppe der sogenannten aromatischen Kohlenwasserstoffe, die, wie es der Name schon sagt, allesamt sehr geruchsintensiv sind und die Basis für alle Parfüme bilden. Die Frage, was derartige Moleküle wohl gemeinsam haben könnten, war lange Zeit ein Rätsel. August Kekulé löste 1865 das Rätsel nachdem ihm im Schlaf die Lösung zugefallen war. Im Traum sah er in seinem Kamin eine Schlange sich winden, die sich selber in den Schwanz biss. Eine ringförmige Struktur war also das Geheimnis, was alle derartigen Moleküle aufweisen. Auch im letzten Jahrhundert gab es noch ähnliche Überraschungen. 1985 wurde ein neuartiges Molekül entdeckt, auf das man sich zunächst auch keinen Reim machen konnte. Fulleren, so nannte man das merkwürdige Gebilde, schien nur aus Kohlenstoffatomen zu bestehen, davon aber gleich 60 an der Zahl ( Abb. 11a ). Nach jahrelangen Studien konnte man schließlich auch hier die Struktur erklären: Das Molekül bildet eine Fußball-Struktur ( Abb. 11b ), d.h. eine Hohlkugel deren Oberfläche von 15 Fünfecken und 20 Sechsecken gebildet wird. Diese Aufklärungs-Leistung wurde 1996 mit dem Nobelpreis belohnt.

Symmetrie als Stilmittel

Im Folgenden wollen wir uns ansehen, wie die Symmetrie von den Malern auf unterschiedliche Weise als Stilmittel eingesetzt wurde. Abb.12 zeigt uns das berühmte Selbstbildnis von Albrecht Dürer. Es ist das erste Selbstbildnis überhaupt. Vorher hatte so etwas noch niemand gemacht oder man sollte vielleicht sagen gewagt, denn als seine Zeitgenossen im Jahre 1500 in Nürnberg des Bildes ansichtig wurden, waren keineswegs alle begeistert. Ja, man hielt es für anmaßend. Dieser Mann mittleren Alters mit den langen Haaren, dem ernsthaften Blick, war das nicht Jesus, Gottes Sohn? Vor allem aber die ausgeprägte Symmetrie entrückte die Gestalt der Normalität des bürgerlichen Lebens. Da half es nur wenig, dass die in die Mitte des Bildes reichende rechte Hand die Symmetrie abschwächte. Später änderte sich die öffentliche Wahrnehmung, und das Bild zählt heute zu den stärksten Portraits, welches die deutsche Renaissance hervorgebracht hat.

Noch stärker als bei Dürer tritt uns die bilaterale Symmetrie im Selbstportrait Ferdinand Hodlers entgegen ( Abb. 13 a ). Der Vergleich mit der Fotografie (Abb. 13b ) belegt, dass dies vom Maler sehr wohl so beabsichtigt war. Ist auf dem Foto der Hemdausschnitt noch leicht nach links versetzt, so ist dieser im Portrait exakt in die Mitte gerückt. Ebenso verstärkt der scharfe Schatten des Revers diesen Eindruck. Das gemalte Bild sagt uns: Hier steht ein tatkräftiger Mann, der sich seiner Begabung durchaus bewusst ist. Hodler, so scheint es, ist als Maler von der Symmetrie geradezu besessen gewesen. Sie spielt in jedem seiner Werke eine gewichtige Rolle. Ein schöner Beleg für diese Behauptung ist das 1904 entstandene Bild vom Thunersee (Schweiz, Abb. 14 ). Hier kommt es durch Spiegelung an der Seeoberfläche zu einer zweifachen bilateralen Symmetrie: Die bilateral symmetrischen Bergketten des südlichen und nördlichen Ufers ergeben ein ebenfalls bilaterales Spiegelbild. Ein wirklich schönes Bild!

Ein früherer Maler, der ebenfalls von der Symmetrie in seinen Bildern oftmals Gebrauch machte, ist Caspar David Friedrich. Abb. 15 zeigt sein vermutlich 1812 geschaffenes Bild „Das Kreuz im Walde“. Mehr noch als in dem kurz davor entstandene Gemälde „Das Kreuz im Gebirge“ hat der Maler hier mit Hilfe der Symmetrie ein religiöses Andachtsbild geschaffen. Inmitten der von einem Quellbach durchflossenen Schlucht steht ein Kreuz, das sich oberhalb der den Hintergrund bildenden Tannen im Himmel als Leuchterscheinung wiederspiegelt. Schlucht und Bäume sind dabei einer starken Symmetrie unterworfen. Ein Kunsthistoriker schreibt dazu: „Das Irdische wird hier überwunden in der transzendenten christlichen Erlösung“.

Von ganz anderer Art ist das zweite Bild (Abb. 16) vom gleichen Maler mit dem Titel „Mönch am Meer“. Sie werden sich zunächst fragen, wo ist denn hier die Symmetrie zu sehen? In der Tat, ist diese nicht sichtbar. Es handelt sich vielmehr um eine abstrakte, spirituelle Form der Symmetrie. Dabei symbolisieren Meer und Strand den Kosmos, dem der denkende Mensch – hier als Mönch – gegenüber steht. Der Betrachter des Bildes ist eingeladen, sich in die Situation des Mönches hinein zu versetzen und mit dessen Augen die Welt zu betrachten.

Was ist Symmetrie ?

Nach diesem ersten Blick auf das weite Feld der Symmetrie wollen wir nun noch einmal auf die anfangs gestellte Frage zurück kommen: Was ist das denn nun eigentlich Symmetrie? Dieser Frage können wir nicht ausweichen, denn für die Anwendung in der Wissenschaft braucht man eine verbindliche Definition. Von den in den Lexika aufgeführten vier Definitionen

Gleich - oder Ebenmaß
Spiegelbildliche Gleichheit
Räumliche oder zeitliche Wiederholung gleicher Elemente
Symmetrie ist die Eigenschaft eines Objektes auf sich selbst abgebildet werden zu können

ist die letzte für die wissenschaftliche Anwendung die wichtigste, da sie die präziseste Aussage macht. Im Zusammenhang mit der Schneeflocke hatten wir schon gesehen, wie so eine Flocke durch Drehung um einen bestimmten Winkel in sich selber überführt werden kann.

Neben der Drehung gibt es aber noch drei weitere Transformationen, die gleiches bewirken:

Drehungen um Symmetrieachse
Translationen (Parallelverschiebungen)
Spiegelungen an einer Ebene
Spiegelungen an einem Symmetriezentrum (Inversionen)

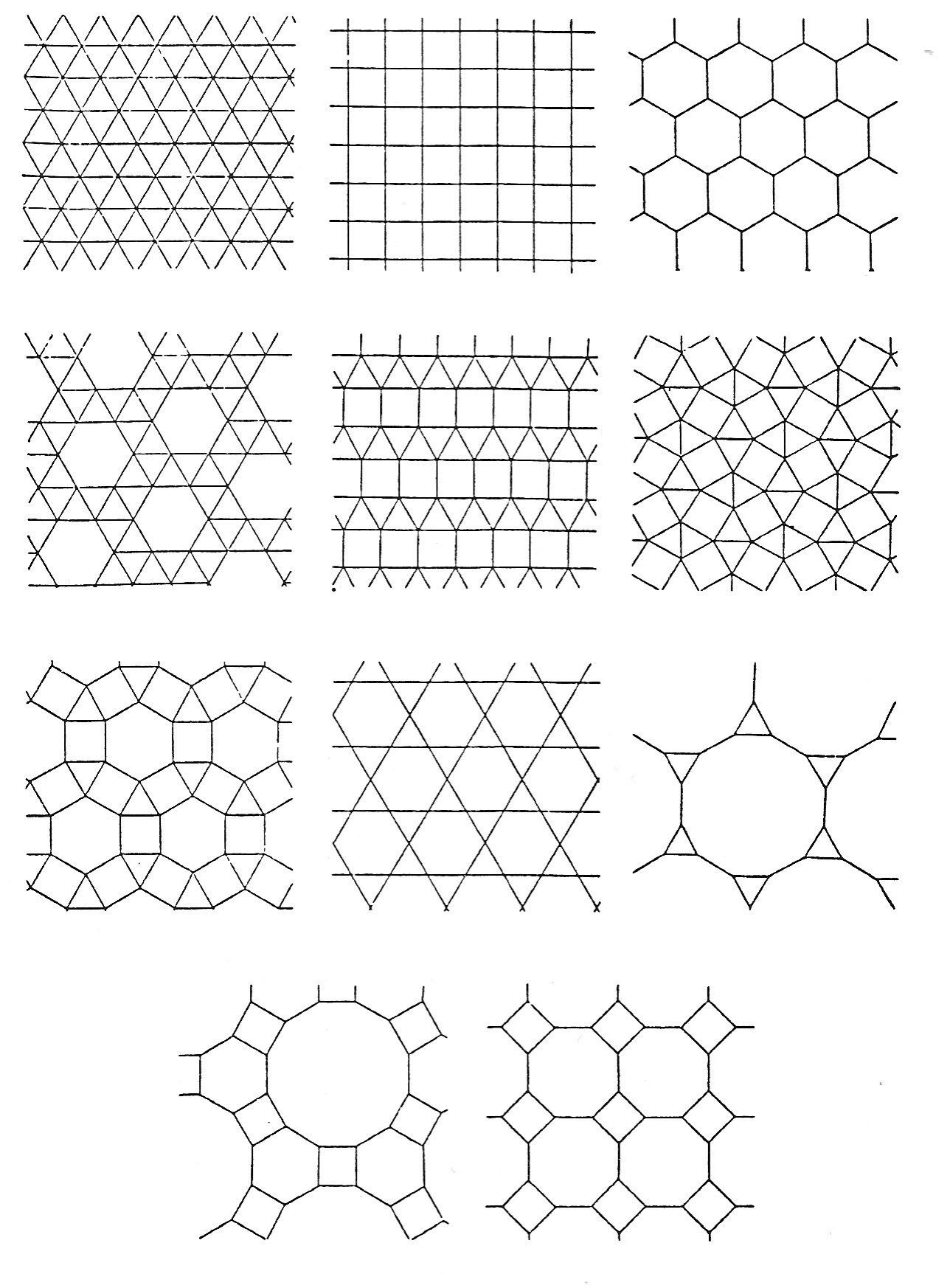
Hinzu kommen noch die Kombinationen wie Drehspiegelungen, Gleitspiegelungen etc. Mathematisch bilden sämtliche Operationen, die ein Objekt auf sich selbst überführen, eine Menge, die man Symmetriegruppe nennt. Die Gruppentheorie, ein Teilgebiet der Mathematik, ist von größter Bedeutung für die Theorie der Kristallgitter und ebenso der Elementarteilchen. Die Wirkung einer Translation kann man sehr leicht an einem gefliesten Fußboden verdeutlichen, wie er in der Abb. 17 zu sehen ist. Das Grundmuster einer derartig symmetrisch aufgebauten Fläche nennt man eine Elementarzelle. Verschiebt man eine solche Zelle um die eine vorgegebene Strecke, so kommt sie mit einer ebensolchen zur Deckung. Die Frage, welche regelmäßigen Vielecke man für eine lückenlose Bedeckung einer Fläche verwenden kann, hat auch Kepler im Zusammenhang mit den Honigwaben beschäftigt. Er erkannte, dass hierzu gleichseitige Dreiecke, Quadrate und Sechsecke geeignet sind, aber keine Fünfecke (Abb. 18 oben). Zählt man die Kombinationsmöglichkeiten von verschiedenen regelmäßigen Polygonen hinzu, so fand er heraus, dass es insgesamt 11 verschiedene Möglichkeiten gibt, eine Fläche zu bepflastern (Abb. 18). Ähnliche Fragen stellen sich bei der Analyse der Kristalle. Wie kommt es beispielsweise zu der Bildung der fünf „Platonischen Körper“: Würfel, Tetraeder, Oktaeder, Dodekaeder und Ikosaeder, die man in der Natur vorfindet? Hier ist ebenso eine möglichst große Packungsdichte der Moleküle im dreidimensionalen Volumen das treibende Prinzip. Auch heute noch bietet die Röntgenbeugung, 100 Jahre nach ihrer Entdeckung durch Max v. Laue (Nobelpreis 1914), eine viel genutzte Methode die Struktur der zahlreichen Kristalle zu untersuchen.

Zum Abschluss dieses eher theoretischen Abschnitts werfen wir noch einen Blick auf die 1928 von Oskar Schlemmer geschaffene Graphik „Rot gegeneinander“ ( Abb. 19 ). Hier sehen wir drei Figuren in rot, die durch Translationen erzeugt worden sind und zum anderen vier weiße, die durch Spiegelungen und Verschiebungen aus diesen hervorgehen.

3. Macht der Symmetrie

Im Folgenden kann es natürlich nicht um die Macht der Politiker, Militärs oder Wirtschaftskapitäne gehen, nein, gemeint ist vielmehr die Macht der Erkenntnis. Genauer, wie man komplizierte Zusammenhänge von einer höheren Warte aus betrachten und damit begreifbar machen kann. Komplizierte Zusammenhänge begegnen uns allenthalben auf den unterschiedlichsten Gebieten, sei es in der Ökonomie, der Klimaforschung oder auch der Dynamik physikalischer Körper. So haben wir es erst in den letzten Tagen wieder erfahren, wie schwierig es ist, die Folgen einer 2,5% Lohnerhöhung in den USA zu beurteilen. Innerhalb weniger Tage entwickelte sich daraus ein handfester Börsen-crash, den kaum jemand vorhergesehen hat. Ebenso ist es ein schwieriges Unterfangen, die Auswirkungen einer erhöhten CO2 Freisetzung auf das globale Klima im Detail zu verstehen. In diesen Fällen kann man zwar Modelle und Gleichungen aufstellen, die die zeitliche Entwicklung beschreiben sollen, aber es verbleiben große Unsicherheiten. Im ersten Beispiel bei der Börse, weil das menschliche Verhalten nicht vorhersehbar ist, im zweiten Fall beim Klima, weil nicht alle Einflüsse – etwa der Wolken oder der Meere – hinreichend bekannt sind.

Bei der Dynamik der Körper hingegen liegen die Dinge anders, in Sonderheit bei den Planeten. Hier kennt man die physikalischen Gleichungen, die die Bewegungen der Körper beschreiben mit extremer Genauigkeit, so dass man – zumindest prinzipiell – den Verlauf der Gestirne über Milliarden von Jahren vorhersagen kann. Diese Gleichungen sind jedoch keine algebraischen Gleichungen, wie man sie aus der Schule kennt, sondern komplizierte Differentialgleichungen, die eigentlich nur eine Anweisung sind, wie man das Ergebnis berechnen kann. Spezielle Fälle kann man mit dem Computer näherungsweise berechnen. In Ausnahmefällen kann man allgemeine Lösungen jedoch auch exakt bestimmen. In solchen Fällen lassen sich die Lösungen durch die Konstanten (Invarianten genannt) der Bewegung beschreiben. Wir werden sehen, dass dies immer möglich ist, wenn Symmetrie vorliegt. Die Kenntnis dieser Invarianten, ist von unschätzbarem Wert: zu wissen, was sich nicht verändert, wenn alle beobachtbaren Größen (Ort, Geschwindigkeit, Winkel, ...) sich ständig verändern.

Die erste physikalische Invariante dieser Art für einen Körper, der sich im Vakuum bewegt, wurde von Galileo Galilei (Abb. 20) experimentell gefunden. Es ist das Produkt von Geschwindigkeit und Masse des Körpers, das wir heute als Impuls (p = m v) bezeichnen. Galilei drückte es mit Worten so aus: Ein Körper verharrt in gleichförmiger Bewegung, solange keine Kraft auf ihn einwirkt. Wir können uns von der Impulserhaltung etwa beim Billardspiel überzeugen. Stößt da eine Kugel zentral mit einer ruhenden zweiten gleicher Art, so bleibt die stoßende Kugel liegen, und die gestoßene rollt mit der Geschwindigkeit der stoßenden weiter.

Einige Jahre später entdeckte Galileis Zeitgenosse, der Astronom Johannes Kepler (Abb. 21) eine zweite Invariante, die man heute Drehimpuls nennt. Kepler war im Jahr 1600 in Prag Assistent des böhmischen Hofastronomen Tycho Brahe geworden. Letzterer hatte während der vorausgehenden zwanzig Jahre sehr sorgfältige Messungen an den damals bekannten Planeten auf der dänischen Insel Ven vorgenommen und wollte nun herausfinden, welche Schlüsse man aus dem umfangreichen Datenmaterial im Hinblick auf die damals noch umstrittene „Kopernikanische Theorie“ ziehen könne. War es tatsächlich so, dass die Sonne und nicht die Erde im Zentrum stand wie Kopernikus es rund 60 Jahre zuvor behauptet hatte. Nur ungern und sehr zögerlich gewährte Brahe dem, ihm mathematisch weit überlegenen Kepler, Einblick in seine Aufzeichnungen. Sein Gesundheitszustand verschlechterte sich jedoch während des Jahres 1601 so dramatisch, dass er, kurz vor seinem Tode, Kepler das gesamte Material übergab, um die Früchte seiner Arbeit zu retten. Damit hatte er eine gute Wahl getroffen, denn kein anderer hätte in der damaligen Zeit daraus so viel erschließen können wie Kepler. Speziell aus der Analyse der Erde- und der Marsdaten konnte er in den folgenden zehn Jahren seine berühmten drei „Keplerschen Gesetze“ ableiten. Wir geben hier nur die zwei ersten wieder (s. auch Abb. 22).

Die Planetenbahnen sind Ellipsen mit der Sonne in einem ihrer beiden Brennpunkte.
Der Fahrstrahl Sonne-Planet überstreicht in gleichen Zeiten gleiche Flächen.

Beide Aussagen wurden keineswegs von den Zeitgenossen anerkennend aufgenommen. So äußerte Galilei, mit dem Kepler eine für damalige Verhältnisse rege Korrespondenz unterhielt, vor allem große Zweifel an der Ellipsenhypothese. Sein Einwand beruhte interessanterweise auf einem Symmetrieargument: Warum sollte ein kugelförmiger Körper wie die Sonne einen anderen kugelförmigen Körper veranlassen, ihn auf einer Ellipse zu umrunden, noch dazu auf einer, wo die Sonne nicht im Mittelpunkt stand? Nein, die Bahn konnte nach seiner Auffassung nur ein Kreis sein. Kepler konnte ihm darauf kein überzeugendes Gegenargument liefern. Es sollten noch 60 Jahre vergehen, bis Isaak Newton, die Richtigkeit aller drei Kepler-Gesetze mathematisch durch Lösung der Kraftgleichung beweisen konnte. Dazu musste zusätzlich zur Anziehungskraft zwischen Sonne und Planet, die schon Galilei und Kepler vermutet hatten, noch die Fliehkraft hinzugenommen werden. Ohne diese von der Sonne wegweisende Kraft würden die Planeten ja auch tatsächlich geradewegs in die Sonne hineinfallen.

Wichtiger für uns im Zusammenhang mit der Symmetrie ist das zweite Gesetz, das auch als „Flächen-Satz“ bekannt ist. Seine Aussage ist äquivalent mit der Erhaltung des Drehimpulses (L=m r^2 ω=const. mit der Winkelgeschwindigkeit ω und dem Radius r). Ist der Abstand von der Sonne (r) groß, so ist die Winkelgeschwindigkeit klein und umgekehrt. Es ist eine direkte Konsequenz aus der Tatsache, dass die auf den Planeten einwirkende Anziehungskraft genau in Richtung Sonne weist, so dass diese Kraft kein Drehmoment auf ihn ausübt, da sie keine Komponente senkrecht zur Verbindungslinie Sonne-Planet aufweist. Ähnlich wie der Impuls eine Erhaltungsgröße ist, wenn keine Kraft auf einen Körper einwirkt, so ist der Drehimpuls eine Erhaltungsgröße, wenn kein Drehmoment auf ihn einwirkt. Eine schöne Demonstration für die Erhaltung des Drehimpulses ist die Pirouette des Eiskunstläufers. Dabei fährt dieser mit ausgebreiteten Armen in eine Kreiselbewegung hinein, wobei er ein Bein am Boden lässt und mit dem zweiten sich vom Boden abstößt. Zieht er nun die Arme zum Körper hin, verkleinert also deren Abstand zum Drehpunkt (Radius), so dreht er sich schneller, die Winkelgeschwindigkeit (Drehfrequenz) nimmt zu. Das umgekehrte passiert, wenn er die Arme wieder ausbreitet.

Es ist noch anzumerken, dass sowohl Impuls als auch Drehimpuls gerichtete Größen (Vektoren) sind, die nicht allein durch eine Zahl charakterisiert werden können. Man kann sie aber graphisch durch einen Pfeil im Raum darstellen. Beim Impuls weist dieser Pfeil in die Richtung der Geschwindigkeit, beim Drehimpuls dagegen ist er parallel zur Drehachse. Schließlich müssen wir bei den Planeten – und so bei der Erde – noch zwischen zwei verschiedenen Drehimpulsvektoren unterscheiden. Was wir nämlich bisher betrachtet haben, ist der sogenannte Bahndrehimpuls, der mit der Bewegung der Erde um die Sonne verbunden ist. Wir können uns ihn anschaulich als einen Pfeil vorstellen, der senkrecht auf der Bahnebene (Ekliptik) steht und seinen Fußpunkt im Sonnenzentrum hat. Daneben verfügt die Erde aber noch über einen Eigendrehimpuls der mit ihrer Rotation um die Erdachse verbunden ist. Dieser ist vom Bahndrehimpuls gänzlich verschieden. Er ist durch einen Pfeil charakterisiert der vom Erdzentrum in Richtung Nordpol weist. Bei der Erde besagt nun die Erhaltung des Eigendrehimpulses, dass die Drehachse immer die gleiche Richtung im Raum beibehält, während die Erde die Sonne umkreist. Damit verdanken wir diesem Erhaltungssatz die unterschiedlichen Jahreszeiten. Im Sommer bescheint die Sonne bevorzugt die nördliche Hälfte der Erde ein halbes Jahr später, im Winter, die südliche Hälfte.

Eigendrehimpulse sind von herausragender Bedeutung für das Verständnis der Mikrowelt also der Welt der Moleküle, Atome und Elementarteilchen. In dieser, von der Quantenmechanik beherrschten Mikrowelt, können die Eigendrehimpulse – hier Spin genannt – nur ganz eingeschränkte Werte annehmen. Misst man die Pfeillängen in einer bestimmten Einheit, so können diese nur ganzzahlig (1, 2, 3...) oder halbzahlig (1/2, 3/2 ,5/2 ...) sein. Teilchen der ersten Sorte nennt man Bosonen, die der zweiten Fermionen; sie zeigen im Kollektiv ein ganz unterschiedliches Verhalten. Während die Bosonen sich zusammendrängen und möglichst nahe beieinander sein wollen, stoßen sich die Fermionen gegenseitig ab. Elektronen, die in allen elektrischen Apparaturen den Strom leiten, sind Spin ½-Teilchen und somit Fermionen. Dagegen sind die Träger des Lichts, die Photonen, Bosonen mit dem Spin 1. Alle Bosonen sind im übrigen Botenteilchen, die Kräfte zwischen den jeweiligen Fermionen vermitteln. So vermitteln die Photonen die elektromagnetischen Kräfte zwischen den elektrisch geladenen Teilchen.

Im 19. Jahrhundert kam die Idee auf, dass es außer Impuls und Drehimpuls noch andere Erhaltungsgrößen geben müsse. Vor allem der außerordentlich begabte Ire, Sir William Rowan Hamilton, revolutioniere in den Jahren 1834-1835 die theoretische Mechanik und erkannte die Bedeutung der Symmetrie für die Auffindung der Invarianten. Den eigentlichen Beweis aber, dass hinter jeder Symmetrie eine entsprechende Erhaltungsgröße steht, lieferte erst Emmi Noether (Abb. 23). Sie wurde 1882 als Tochter jüdischer Eltern in Erlangen geboren. An der dortigen Universität hatte ihr Vater einen Lehrstuhl für Mathematik inne. Nach ihrer Promotion an der gleichen Universität bei Prof. Gordan im Jahr 1907 im Fach Mathematik wurde sie 1909 von den Koryphäen Felix Klein und David Hilbert nach Göttingen, dem „Mekka“ der Mathematik, gerufen. Obwohl von beiden nachhaltig empfohlen, wurde ihr 1915 eingereichter Antrag auf Habilitation abgelehnt: Frauen waren damals noch nicht zur Habilitation zugelassen – das änderte sich erst während der Weimarer Republik. Als Assistentin von Hilbert publizierte sie 1918 unter dem Titel „Invariante Variationsprobleme“ das „Noethersche Theorem“. Es lautet: Zu jeder kontinuierlichen Symmetrie eines physikalischen Systems gehört eine Erhaltungsgröße.

Nachdem ihr 1933 durch das Naziregime die Lehrerlaubnis entzogen wurde, ging sie in die USA. Dort lehrte sie als Gastdozentin am Women’s College Bryn Mawr in Pennsylvania. Bereits 1935 verstarb sie dort nach einer Unterleibsoperation. Danach wurde ihre Arbeit lange Zeit kaum gewürdigt. Das änderte sich erst 40 Jahre später als sich die Physik der Erforschung der Elementarteilchen zuwandte, wo es neue Symmetrien zu entdecken gab. Heute ist das Noethersche Theorem einer der wichtigsten Lehrsätze der modernen theoretischen Physik. Wir entnehmen der unteren Zusammenstellung, dass auch der so bedeutsame Erhaltungssatz für die Energie auf eine zeitliche Symmetrie zurück zu führen ist.

Homogenität des Raumes –> Impulserhaltung
Isotropie des Raumes. –> Drehimpulserhaltung
Homogenität der Zeit –> Energieerhaltung
Homogenität des Potentials –> Erhaltung der elektrischen Ladung
Farbsymmetrie –> Erhaltung der Farbladung
etc.

Die Spiegelwelt der Antiteilchen

Neben den leicht zu erkennenden kontinuierlichen Symmetrien wie Homogenität und Isotropie gibt es verborgene Symmetrien, die schwieriger zu erkennen sind. So wusste man durch die Jahrtausende der Menschheitsgeschichte nichts von der Existenz der Antiteilchen. Die Erkenntnis, dass derartige Spiegelteilchen existieren können verdanken wir einer theoretischen Vorhersage von Paul Dirac (Abb. 24). Ihm war es gelungen, in einem ersten Schritt die Quantenmechanik mit der Relativitätstheorie zu verknüpfen. Seine heute als Dirac-Gleichung bekannte Gleichung ist somit eine Erweiterung der Schrödinger-Gleichung, die der Bedingung Rechnung trägt, dass kein massebehaftetes Teilchen die Lichtgeschwindigkeit erreichen kann. Als er 1928 eine erste Lösung dieser Gleichung fand, stellte er mit Erstaunen fest, dass diese neben den erwarteten positiven Energiewerten auch ebensolche mit negativem Vorzeichen aufwies. Lange wurde gerätselt, was dieses nun zu bedeuten habe. Dirac kam schließlich zu der Erkenntnis, dass es neben den bekannten negativen Elektronen potenziell auch solche mit gleicher Masse aber positiver Ladung geben könne. Die Naturgesetze würden jedenfalls damit nicht im Widerspruch stehen. Und tatsächlich, bereits vier Jahre später, wurden diese Positronen genannten Teilchen von C. D. Anderson in der kosmischen Strahlung nachgewiesen. Sie können mittlerweile leicht technisch in großer Zahl erzeugt werden und finden heute als Positronen-Strahl in der Krebsbekämpfung eine wichtige Anwendung. Ebenso können heutzutage auch Antiprotonen und alle andere Antiteilchen, ja sogar ganze Antiatome in den großen Beschleunigungsanlagen hergestellt werden. Dabei besteht eine vollständige Symmetrie, so ist das Antiteilchen des Positrons wieder ein Elektron. Masse, Lebensdauer und Spin eines Teilchens und seines Antiteilchens sind gleich, ebenfalls Art und Stärke ihrer Wechselwirkungen. Hingegen sind elektrische Ladung, magnetisches Moment und alle ladungsartigen Quantenzahlen entgegengesetzt gleich (s. Abb.25). So könnte es durchaus eine Welt geben, die vollständig aus Antiteilchen aufgebaut ist. Denkbar ist es demnach auch, dass ferne Galaxien, möglicherweise sogar die Hälfe von ihnen, aus Antimaterie bestehen. Aber wehe, wenn eine Galaxie in eine Anti-Galaxie eindringen würde! Dann würden sich beide auslöschen. Jedes Paar aus Teilchen und Antiteilchen zerstrahlt nämlich, wenn sie sich zu nahe kommen. Die in ihren Massen gespeicherte Energie (E=2m c^2) wird dabei in zwei Photonen mit gleicher Energie umgewandelt. Wir werden auf diesen Zerstrahlungsprozess (Annihilation) gegen Ende noch einmal zurück kommen.

4. Symmetriebrechung in der Kunst und in der Wahrnehmung

Wir wollen uns nun dem ebenfalls wichtigen Phänomen der Symmetriebrechung zuwenden. Zuerst vier Beispiele aus der Malerei. Bei dem ersten Bild (Abb. 26 ) zu diesem Aspekt handelt es sich um ein Stillleben aus dem Jahr 1973, gemalt vom Bruder des Autors, Klaus Fußmann. Bei diesem ruhigen Bild sticht uns sofort der Teller auf der rechten Bildseite ins Auge. Er ist keineswegs rund und das mit Absicht nicht. Wäre er nämlich kreisrund symmetrisch, wie das ja bei einem fabrikgefertigten Teller zu erwarten wäre, verlöre das Bild erheblich an Spannung. Hier wurde also die Symmetriebrechung mit Bedacht eingesetzt, um die Attraktivität zu erhöhen.

Auf dem folgenden Bild „Verbotene Reproduktion“ ( Abb. 27 ) vom belgischen Maler René Magritte 1937 gemalt, sehen wir einen Mann vor einem Spiegel. Aber was ist das für ein merkwürdiger Spiegel? Das auf der rechten Seite liegende Buch spiegelt sich darin, wie man es erwartet, aber mit dem Mann stimmt was nicht! Anstelle seines Spiegelbildes von vorn, sehen wir im Spiegel ebenfalls seine Rückseite – irritierend, aber zugleich auch faszinierend!

Sodann betrachten wir ein Bild von Salvador Dali ( Abb. 28 ) aus dem Jahr 1945 mit dem Titel „Melancolia“. Eine Frau (Isabel Styler-Tas) betrachtet ihr Spiegelbild. Ihr wird eine surreale Metamorphose gegenübergestellt, ein Spiegelbild in Auflösung. In der Mitte erzeugen zwei extrem hohe Krücken einen bilateralen Symmetrieeindruck. Das Bild charakterisiert Dalis Weltsicht: Tod und Leben, Traum und Wirklichkeit sind immer dicht beieinander.

Das vierte und letzte Bild in diesem Kontext ist die von Arnold Böcklin 1886 gemalte Toteninsel (Abb. 29 ). Böcklin hat diese Szene fünfmal gemalt, wobei die hier gezeigte Fassung diejenige mit der größten Symmetrie darstellt. Das Einfahrtstor für den Kahn mit Ruderer sowie einer in Weiß gehüllten hohen Figur mit dem davor liegenden Sarg, bilden zwei mächtige, symmetrisch angeordnete Säulen. Die sich nach links und rechts anschließenden Mauern und ebenso die Baumgruppe im Hintergrund wie auch die wunderbar vom Mondlicht erhellten linken und rechten Partien des Gebäudes betonen ebenfalls diese Symmetrie. Dagegen unterliegen die Fenster des Gebäudes keiner Symmetrie. Das Bild traf bei den Zeitgenossen auf große Zustimmung. Vermutlich wegen der visionären Abgeschiedenheit, die den Gefühls- und Phantasiebedürfnissen der Menschen damals, wie heute entgegen kommt.

Spektakulär und immer wieder zum Staunen Anlass gebend, sind Zeichnungen, in denen es zu Brüchen in der Wahrnehmung kommt. Das hier gezeigte Beispiel ( Abb. 30 ) kann sowohl als junge oder auch als alte Frau wahrgenommen werden, jedoch nicht beides gleichzeitig. So wird aus dem Halsband der Jungen der Mund der Alten und aus dem Kinn der Jungen die Nase der Alten. Der Wille unseres Gehirns, in einem Bild etwas schon Bekanntes wieder zu erkennen, lässt in unserem Kopf gleichsam einen Schalter umlegen, entweder das eine oder das andere, aber nicht beides: die Symmetrie alt/jung muss gebrochen werden. Wir werden sehen, dass diese Symmetriebrechungen in der Wahrnehmung ein Pendant finden in den Phasenübergängen bei physikalischen Prozessen.

5. Symmetriebrechung in der Physik

Den wahrscheinlich einfachsten Fall der Symmetriebrechung in der Physik finden wir bei einem senkrecht aufgestellten Bleistift ( Abb. 31 ). Auch wenn wir uns noch so viel Mühe geben, er wird nach kurzer Zeit umfallen und auf der Tischplatte zur Ruhe kommen. Aus der anfänglich instabilen, senkrechten Lage kommt er schließlich in der waagerechten zur Ruhe. Physikalisch ist diese Gleichgewichtslage ein Zustand minimaler potentieller Energie (Eend = 0), während in der Ausgangsposition diese ein Maximum aufweist (Eo= m g h/2, mit der Stiftlänge h und der Erdbeschleunigung g = 9,81 m/s2). Die Energiedifferenz (Eo-Eend) hat der Bleistift beim Aufprall an die Tischoberfläche abgegeben. Geometrisch betrachtet ist der Stift aus der symmetrischen Anfangsposition (alle Fallrichtungen sind gleichwahrscheinlich, also isotrop) in die unsymmetrische Lage auf dem Tisch übergegangen, die durch einen bestimmten Winkel in der Tischebene gekennzeichnet ist. Wir können also festhalten, dass die Symmetriebrechung den Körper in einen Zustand mit erniedrigter Energie überführt.

Etwas ganz Analoges vollzieht sich auch bei dem komplizierteren Fall der Magnetisierung. Hier betrachten wir einen Stabmagneten, der an einem Ende den magnetischen Nordpol und am gegenüberliegenden den Südpol aufweist ( Abb. 32 ). Erwärmen wir ihn auf eine Temperatur oberhalb der sogenannten Curie-Temperatur (760°C bei Eisen, 360° bei Nickel), so verliert er seine magnetische Eigenschaft. Lassen wir ihn danach jedoch wieder abkühlen, so wird er wieder magnetisch (auch ohne äußeres Magnetfeld), jedoch können nun Nord- und Südpol gegenüber dem Anfangszustand vertauscht sein. Was ist passiert? In der Abb. 32 geben wir die Erklärung. Der Stabmagnet besteht in Wirklichkeit aus einer sehr großen Zahl winziger Stabmagnete. Diese zeigen bei hoher Temperatur in die verschiedensten Richtungen, so dass er nach außen wie ein Nichtmagnet erscheint. Senken wir nun die Temperatur ab, so kommt es bei Unterschreiten der Curie-Temperatur zu einer kollektiven Wechselwirkung, resultierend in einer Ausrichtung der kleinen Magnete im Innern, so dass auch außen ein Magnetfeld in Erscheinung tritt. Es handelt sich um einen Phasenübergang von der nicht-magnetischen in die magnetische Phase. Wir können aber auch sagen, es hat eine Symmetriebrechung stattgefunden: aus dem ungeordneten, entmagnetisieren Zustand (isotrope Verteilung der kleinen Magnete, hohe Symmetrie) ist ein geordneter Zustand (gebrochene Symmetrie) entstanden.

Symmetriebrechung im Urknall

Die zuvor besprochenen Sachverhalte sollen uns nun helfen, auch einige Dinge zu verstehen, die sich in der allerersten Anfangsphase unseres Weltalls, also im Urknall, zugetragen haben. Nach anfänglichen Unsicherheiten hat sich in den letzten Jahren die Zeitdauer, wie lange dieses Ereignis zurückliegt auf 13,8 Milliarden Jahre eingependelt. Die überwiegende Zahl der Experten ist heute der Auffassung, dass mit dem Urknall auch Zeit und Raum erst entstanden sind. Warum es den Urknall gegeben hat, und was davor gewesen sein mag, wissen wir nicht, obwohl auch dazu allerlei Spekulationen im Umlauf sind. Außer Zweifel scheint jedenfalls, dass während der absoluten Frühphase, der sogenannten Planck-Ära (t< 10^(-43) s), die räumliche Ausdehnung wahrhaft winzig (wesentlich kleiner als ein Atom) und die Temperatur der Urmaterie extrem hoch (T > 10^32 K) gewesen sein müssen. In dieser Frühphase gab es weder Atome noch die uns heute bekannten Elementarteilchen. Es lag ein Zustand vor, den man als Supersymmetrie bezeichnet, was bedeuten soll, dass alle Teilchen masselos wie die Lichtteilchen (Photonen) und praktisch alle von der gleichen Art waren, denn Fermionen und Bosonen konnten sich noch ständig ineinander umwandeln. Mit der rasant zunehmenden Ausdehnung des Raumes war aber auch eine rasche Abkühlung verbunden, und nach etwa einer Mikrosekunde geschah etwas Ähnliches wie bei der Magnetisierung, wenn die Temperatur unter den Curie-Punkt abfällt: Es kam zu einer spontanen Symmetriebrechung und das sogenannte Higgsfeld entstand. Es ist seitdem im gesamten Kosmos zugegen. Wir merken von diesem Higgsfeld nichts. Kann es denn dann überhaupt in der Wirklichkeit vorhanden sein? Aber vom Magnetfeld der Erde bemerken wir ja auch nichts; es ist weder sichtbar noch sonst mit den Sinnen erfassbar. Nehmen wir aber eine Kompassnadel zur Hand, so sehen wir, dass sie überall auf der Erde und auch noch in tausend Kilometer Höhe in Richtung Nordpol weist. Der leere Raum, das Vakuum, ist anscheinend gar nicht so gänzlich leer, wie wir meinen, er kann Eigenschaften annehmen, die man mit dem Feldbegriff beschreiben kann. Allerdings ist das Higgsfeld von gänzlich anderer Natur als ein Magnetfeld. Es hat vor allem die Fähigkeit, den Teilchen Massen zuzuweisen. Das hat es bereits in der ersten Mikrosekunde nach dem Urknall getan, und es entstanden zunächst die schweren Quark-Teilchen, aus denen sich später die Protonen und Neutronen bildeten, die wir auch heute noch finden. Aber nicht nur diese, sondern zu jedem Teilchen stand auch das entsprechende Anti-Teilchen zur Verfügung. Dann aber setzte ein gewaltiger Vernichtungsakt ein. Wie zuvor erwähnt, zerstrahlen Teilchen und Antiteilchen, wenn sie miteinander stoßen indem sie in zwei Photonen zerfallen. In einer späteren Phase, etwa 1 Sekunde nach dem Urknall, bildeten sich auch die wesentlich leichteren Elektronen und Positronen, die sich ebenfalls durch Zerstrahlung vernichteten. Die gesamte Materie wurde so in Licht umgewandelt. Die ganze? Nein, nicht die ganze, aber fast. Ein winziger Rest von einem Milliardenstel der normalen Teilchen blieb übrig und daraus entstanden alle Sterne, Planeten und Staubwolken, die wir heute noch im Kosmos beobachten können und natürlich auch wir Menschen. Warum war das so? Wir wissen es nicht. Man mag sagen, ein Bruchteil von einem Milliardenstel ist ja auch wahrlich nicht viel. Aber generell arbeitet die Natur mit einer uns unvorstellbaren Exaktheit. So ist die Zahl der negativ geladenen und der positiv geladenen Teilchen im Weltall wesentlich genauer bilanziert, und zwar mindestens bis auf 19 Stellen nach dem Komma. Anderenfalls würden nämlich die elektrischen Kräfte und nicht die Gravitationskräfte das Geschehen im Kosmos bestimmen, so dass es weder Planetensysteme noch Doppelsterne geben dürfte. Wäre aber nur der Bruchteil 10^-19 aller Teilchen übrig geblieben, so wäre die Zahl der Sterne im Kosmos um den Faktor 10^-19/10^-9 = 10^-10 verringert und an Stelle der 100 Milliarden Sterne in der Milchstraße würde diese nur etwa 10 Sterne aufweisen!

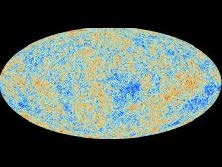
Wie auch immer, was ist mit all der Strahlung passiert, die damals entstanden ist. Die Antwort ist, sie ist immer noch vorhanden, und wir können sie auch beobachten. Sie bildet die sogenannte kosmische Hintergrundstrahlung, die 1964 zufällig von A. Penzias und R.W. Wilson entdeckt wurde (Nobelpreis 1978). Es handelt sich um eine Mikrowellenstrahlung (mit Wellenlängen im mm Bereich), die den ganzen Kosmos isotrop erfüllt. Sie erscheint uns aber, als käme sie von einer kalten (T = 2,78 K) kugelförmigen Wand in einer Entfernung von 13.8 Milliarden Lichtjahren. Dabei ist die Richtungsunabhängigkeit der Intensität wirklich phänomenal: die stärksten Abweichungen vom Mittelwert betragen nur 0,1%. Die Verteilung dieser Strahlung über den gesamten Himmel wurde in den letzten 20 Jahren in drei Satelliten-Missionen mit immer höher Genauigkeit vermessen. Das Ergebnis der 2013 beendeten „Planck-Mission“ sieht man in der Abb.33 . Es zeigt die Verteilung der Strahlung über den gesamten Himmel 380 000 Jahre nach dem Urknall. Zu diesem Zeitpunkt war die Temperatur auf etwa 4000 K abgefallen und aus den Elektronen und Protonen konnten sich durch einen Vorgang, den man Rekombination nennt, stabile Wasserstoffatome bilden. Damit wurden die zuvor freien Elektronen gebunden und der Kosmos wurde transparent. Ein Vorgang, vergleichbar mit der Auflösung des Frühnebels, der uns plötzlich die freie Sicht auf die Umgebung gewährt. Übrigens sind die rötlichen Stellen in der Abb.33 die Positionen mit geringfügig erhöhter Temperatur; es sind gleichzeitig Gebiete in denen sich die Materie verdichtet hatte. Aus ihnen bildeten sich im Laufe der folgenden Milliarden von Jahren die Galaxien. Aus einer statistischen Analyse der Verteilung der Flecken (mittlerer Winkelabstand etwa 1°) lässt sich u.a. mit großer Genauigkeit die Zeit bestimmen, die seit ihrer Bildung vergangen sind, es sind die schon genannten 13,8 Milliarden Jahre.

Schlussbemerkungen

Meine sehr verehrten Damen und Herren, im Vorausgehenden habe ich versucht, Ihnen einen Eindruck zu vermitteln, welche Bedeutung der Symmetrie in der Kunst und in der Wissenschaft zukommt. Abgesehen davon, dass es – wie erwartet – nicht möglich war, hier zu einer auch nur annähernd vollständigen Wiedergabe der in beiden Feldern vorliegenden Materialien zu gelangen, muss ich mir eingestehen, dass es mir leider nicht gelungen ist, in der Symmetrie ein tieferes geistiges Band zu erkennen, dass Kunst und Wissenschaft verbindet. Zwar gibt es zahlreiche Analogien, wie etwa das Phänomen der Symmetriebrechung, doch ist es auch hierbei nicht so, dass das Verständnis der verschiedenen Anwendungen im Bereich der Kunst sogleich den Erkenntnisschlüssel für die entsprechenden wissenschaftlichen Vorgänge liefert.

Trotz dieser etwas enttäuschenden Feststellung bin ich aber keineswegs unglücklich, viel Zeit und Mühe in diese vergleichende Arbeit investiert zu haben. Allein die Betrachtung der verschiedenen Kunstwerke und ihre Interpretation war für mich gleichermaßen amüsant wie bildend. So hoffe ich, dass auch Sie als Zuhörer, den Vortrag als einen gewinnbringenden Bericht über ein faszinierendes Thema erlebt haben und nicht ganz ohne Erkenntnisgewinn auf dem einen oder anderen Gebiet von dannen gehen.